公開日：2020年09月25日
| 更新日：2024年03月14日

「PLLのループフィルターってどうやって決めるの？」気を付けるべき３つのポイント

ライター：mtmt
クロック

はじめに

シリアル通信の高速化に伴い、システムクロックのジッタに関する要求が厳格化しています。この厳しい要求に応えるため、PLL技術を使ったジッタクリーナICが広く使われるようになりました。ジッタークリーナやPLLの設計をしているときに、ループフィルターの設計に困った経験はありませんか？？(当然私もその中の一人になります。)PLLループ帯域の最適化には、ループフィルターの最適な設計が必要となります。

この資料では、ループ帯域とループフィルターの関係性及び、最適なループフィルターの設計に必要な３つのポイントについて解説します。加えて、TI社から提供されるPCベースのPLLシミュレーションソフト、PLLatimumを使い、最適なループ帯域を実現するループフィルター設計事例も紹介します。

PLLの原理

3つのポイントの説明の前に、PLL(Phase Lock Loop：位相同期回路)の説明になります。PLLはフィードバック方式を用いた発振回路で、以下の用途で使われます。

リファレンスクロックから様々な周波数のクロックを合成
リファレンスクロックに含まれるジッタを除去
入力信号からクロックを再生

(詳細は以下のブロック図になります)

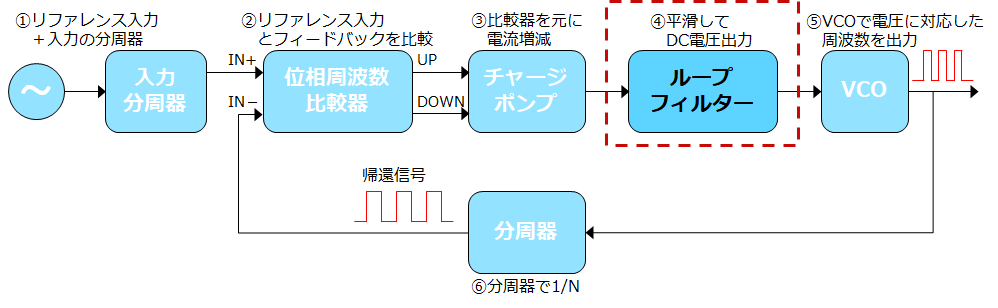
図.１　PLL概略図

PLLは様々な電子機器、例えば、無線機器の発振源や通信機器のクロック再生、放送機器のジッター除去等に使われます。PLLの設計で重要になるのがループフィルターです。ループフィルターはチャージポンプの出力を平滑するローパスフィルターと、カットオフ周波数Fcを決める働きがあります。ループ帯域は、位相追従速度と位相ノイズ性能に影響します。最適に設計したループフィルターは出力の位相ノイズ低減に寄与します。最適なループフィルターを設計する際、気を付けるべき点を説明します。

何が最適なループフィルターか？気を付けるべき３つのポイント

最適なループフィルターとは以下の３つの条件を満たすことです。

フィードバック系が発振しない係数の選択
出力位相ノイズを最小化するループ帯域の選択
短いロック時間

これらの要求は矛盾するため、各要求性能の間で妥協点(トレードオフ)を見出す必要があります。それぞれの条件について詳しく見て行きます。

①フィードバック系が発振しないためには位相余裕は45°～89°が必要

位相余裕が小さい(例として30度)と、リンギングが発生して位相ノイズが増大し、最悪フィードバック系が発振し、障害の原因になる可能性が有ります。一方、位相余裕が大きすぎると、収束に時間が掛かりPLLロック時間が長くなります。

■位相余裕-時間の関係

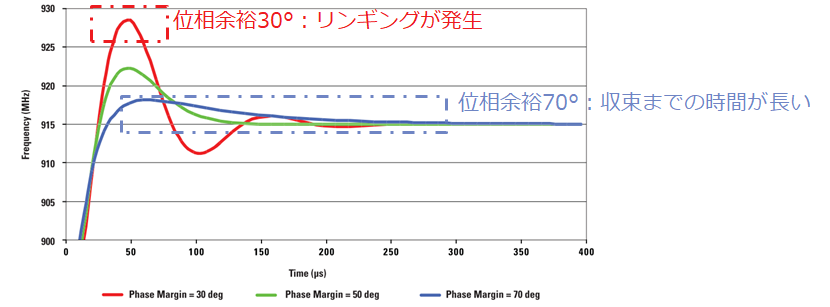
図.２　位相余裕と時間の関係

出典：Texas Instruments – Document『Clock Conditioner Owner’s Manual SNAA103』

■位相余裕－各オフセット周波数での位相ノイズ

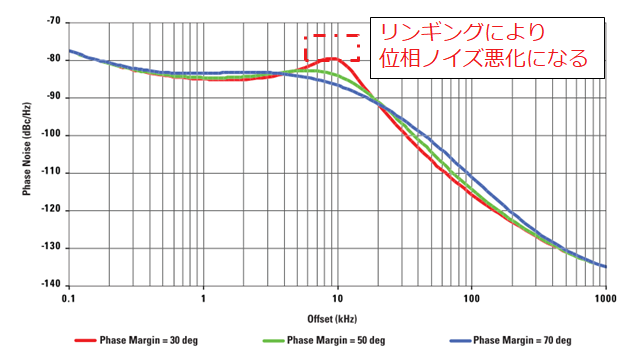
図.３　位相余裕とオフセット周波数での位相ノイズ

出典：Texas Instruments – Document『Clock Conditioner Owner’s Manual SNAA103』

　一般的に以下を目安に従い妥協点を見つけます。

位相ノイズを可能な限り抑えたい：位相余裕を70度
収束(Lock時間)を優先したい：位相余裕を45度
汎用的な用途：位相余裕を50～60度程度

②出力位相ノイズを最小化するループ帯域の選択

PLLのループ帯域の定義はオープンループ利得(G(ω))と分周比(N=1/H)の逆数の積の絶対値が１になる周波数です。
|G(ω)・H|=1

つまり、ループ利得が0dB(=1倍)になるまでの周波数がループ帯域です。

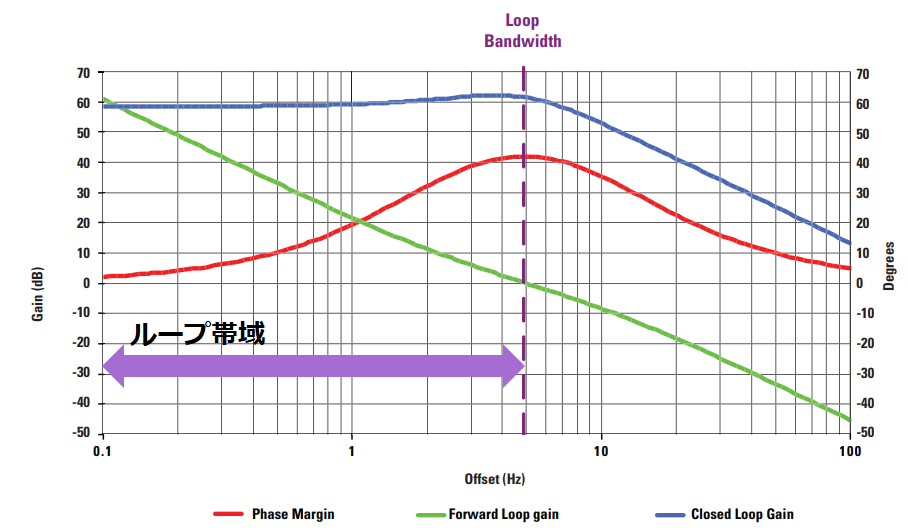
図.４　カットオフ周波数

出典：Texas Instruments – Document『Clock Conditioner Owner’s Manual SNAA103』

③短いロック時間

一般的に、ループ帯域は以下で設定します。

位相比較周波数(fcomp)/1,000～位相比較周波数(fcomp)/20,000

ループ帯域を決める際に、以下のトレードオフが生じます。

■ループ帯域を狭くする
入力リファレンスに含まれるループ帯域以上の位相ノイズを軽減し、PLL出力に含まれるジッターを改善します。

■ループ帯域を広くする
VCOに含まれるループ帯域以下の位相ノイズを軽減します。また、Lock時間を短縮できます。

PLL各部で発生するノイズとループ帯域の関係とは？

設計で気を付けるべき3点は今まで述べた通りになります。一方でPLL各部で発生するノイズが、ループ帯域により、どの様に出力に影響するか、詳しく見て行きます。
下の図はノイズのない理想的なPLLのモデルです。

■理想モデル

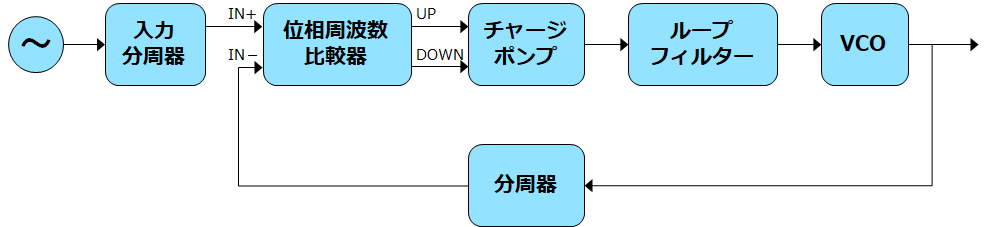
図.５　PLL理想モデル

出典：Texas Instruments – Document『Clock Conditioner Owner’s Manual SNAA103』

これに対し、PLL各部で発生するノイズを加えたものが下の図です。

■実際のモデル

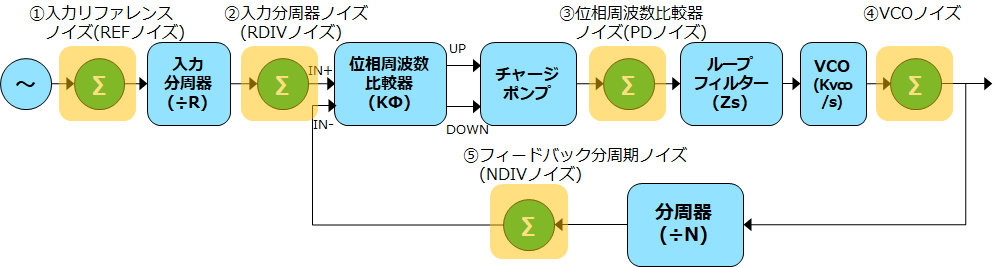
図.６　PLL実際のモデル

出典：Texas Instruments – Document『Clock Conditioner Owner’s Manual SNAA103』

ここでPLLの伝達特性を求めます。PLLのオープンループ利得G(s)は次式で示されます。

$\begin{align*} \left G(s)= \frac{(K \Phi\times KVCO\times Z(s))}{s} = \frac{(K \Phi\times KVCO\times Z(s))}{j2πf} \end{align*}$ ※ VCO利得は係数sで除算します。VCOの出力周波数で、それを位相に戻すためです。虚数jの絶対値を取ると、以下になります。

$\begin{align*} |G(s)| = \frac{(K \Phi\times KVCO\times Z(s))}{2\pi f} \end{align*}$

オープンループ利得|G(s)|は周波数fに反比例します。
周波数増加とともにオープンループ利得|G(s)|は減少します。

クローズドループ利得Cl(s)は次式で示されます。

$\begin{align*} Cl(s)= \frac{G(s)}{1+G(s)} \end{align*}$

フィードバックデバイダ(分周器N)を考慮したクローズループ利得Cl(s)は次式で示されます。

$\begin{align*} Cl(s)= \frac{G(s)}{1+ \frac{G(s)}{N}} \end{align*}$

便宜上、分かりやすい表示のためH=1/Nとすると、上式は以下になります。

$\begin{align*} Cl(s)= \frac{G(s)}{1+G(s) \times H} \end{align*}$

オープンループ利得G(s)|はループ帯域より低い周波数領域では、1<<G(s)、ループ帯域より高い周波数領域では１>>G(s)の関係が成り立ちます。

下の表で、伝達関数の行は、各ノイズ源が出力に現れる際の伝達関数を示します。ループ帯域より低い周波数領域、並びに、高い周波数領域について、上記関係を使い近似式を求めます。

ノイズ源	伝達関数	ループ帯域より低い周波数領域 1<<G(s)	ループ帯域より高い周波数領域 1>>G(s)
VCO	$\begin{align} \frac{1}{1+G(s) \times H} \end{align}$	$\begin{align} \frac{1}{1+G(s) \times H} \fallingdotseq \frac {1}{G(s)} \times N \end{align}$	$\begin{align} \frac{1}{1+G(s) \times H} \fallingdotseq 1 \end{align}$
入力リファレンス	$\begin{align} \frac{1}{R \times CL(s)} \end{align}$	$\begin{align} \frac{1}{R} \times \frac {G(s)}{1+G(s) \times H} \fallingdotseq \frac{N}{R} \end{align}$	$\begin{align} \frac{1}{R} \times \frac{G(s)}{1+G(s) \times H} \fallingdotseq \frac{G(s)}{R} \end{align}$
入力分周器	CL(s)	$\begin{align} \frac {G(s)}{1+G(s) \times H} \fallingdotseq N \end{align}$	$\begin{align} \frac{G(s)}{1+G(s) \times H} \fallingdotseq G(s) \end{align}$
フィードバック分周器	CL(s)	$\begin{align} \frac{G(s)}{1+G(s) \times H} \fallingdotseq N \end{align}$	$\begin{align} \frac{G(s)}{1+G(s) \times H} \fallingdotseq G(s) \end{align}$
位相比較器	$\begin{align} \frac{1}{K \phi \times CL(s)} \end{align}$	$\begin{align} \frac{1}{K \phi}\times \frac{G(s)}{1+G(s) \times H} \fallingdotseq \frac {N}{K \phi} \end{align}$	$\begin{align} \frac{1}{K \phi}\times \frac{G(s)}{1+G(s) \times H} \fallingdotseq \frac {G(s)}{K \phi} \end{align}$

ループ帯域より低い周波数領域：

PLL各ブロックに起因するノイズの中で、特にリファレンスに含まれるノイズが支配的です。

ループ帯域より高い周波数領域：

PLL各ブロックに起因するノイズの中で、VCOノイズが支配的です。

上記から、入力リファレンスとVCOの位相ノイズを把握し、最適なループ帯域を選定することでPLL出力の位相ノイズを最小化できます。

PLLatinumを用いたループ応答最適化事例

TI社のクロック製品に関しては、同社が提供するアプリケーションソフト”PLLAtinum”を使えば、ループのボーデ線図、ループの位相余裕、位相ノイズ等を可視化でき、最適なループフィルターを見出すことができます。

ループフィルターに使用するコンデンサ、抵抗の定数を知ることもできます。

PLL定数設定画面

PLL定数設定画面では、主に以下の各定数設定を行います。

ループフィルターのRC定数
入出力周波数(分周比含む)
出力形式(LVDS, LVCMOS, LVPECL)
VCO周波数

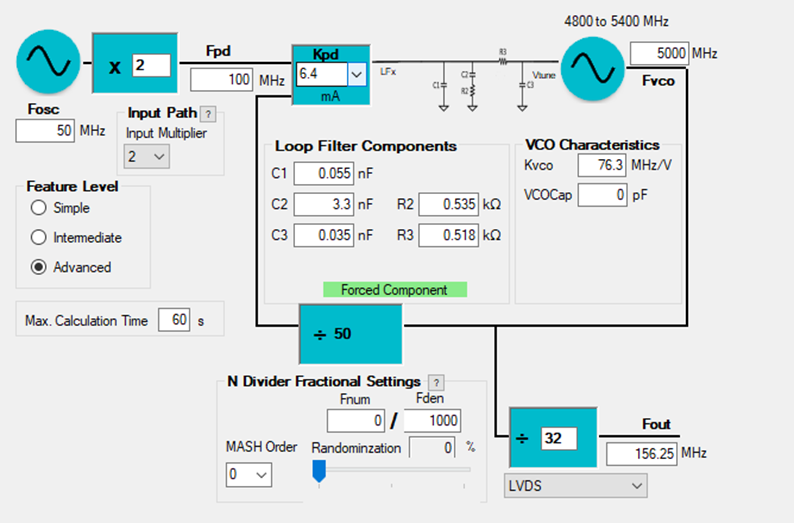
図.７　PLLatinum 設定画面

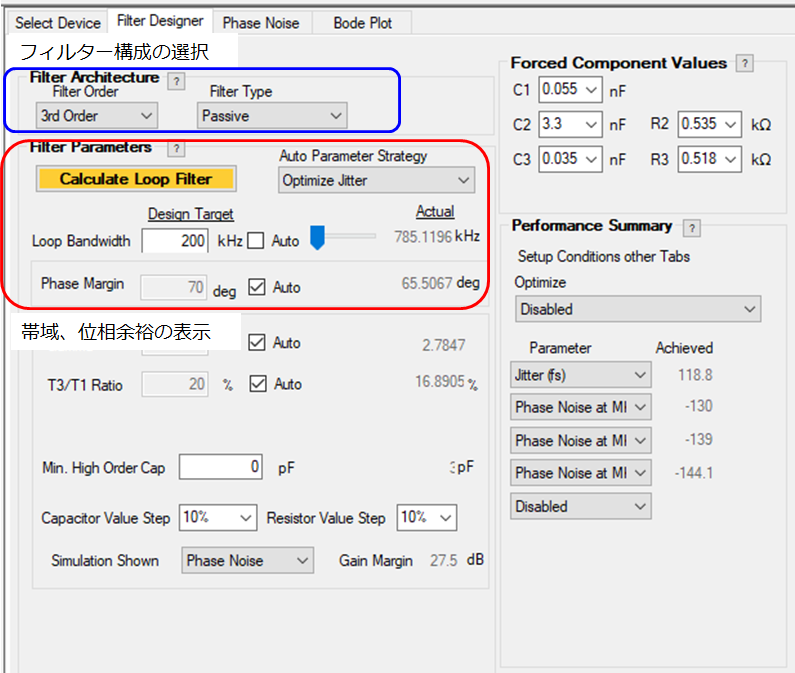
ループフィルター設定

この画面はループフィルター定数設定画面になります。

フィルター構成の選択(2nd～4th)
ループフィルターの帯域設定

設定されたRC定数でのループ帯域で計算結果が表示されます
位相ノイズも数値表記します
※ Auto選択すると最適なフィルターが自動構成されます

Jitter優先、Lock時間優先等、ユーザーの希望に合わせてカスタマイズできます。

位相ノイズ特性表示(グラフ)

設定したループフィルターにて位相ノイズ特性を簡易的に可視できます。

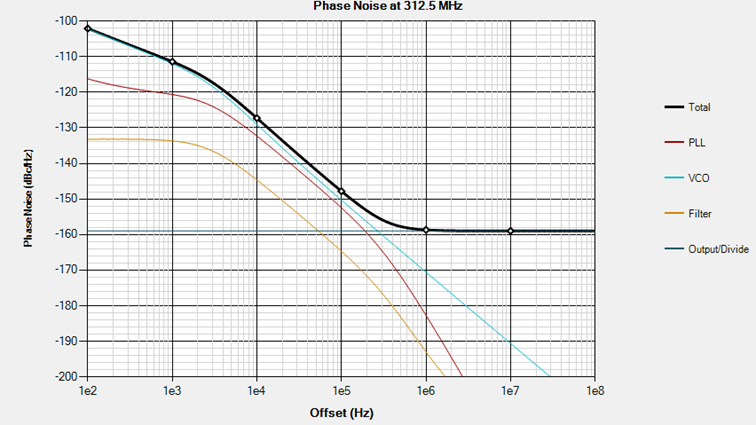
図.８　PLLatinum位相ノイズ特性表示(グラフ)

位相ノイズ特性表示(数値表示)

各オフセット周波数での位相ノイズ、RMSジッターも確認できます。クロックソース源に各オフセット周波数の位相ノイズを入力することも可能です。

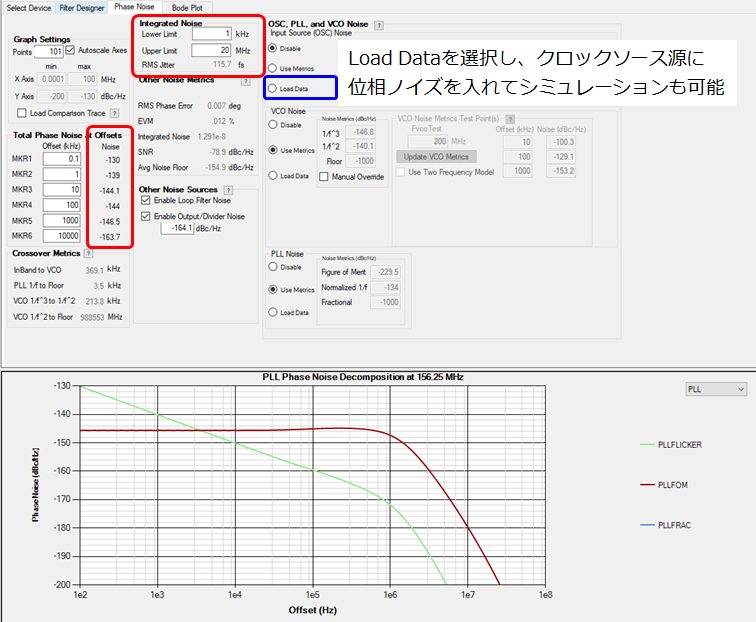
図.９　PLLatinum位相ノイズ特性表示(数値表示)

まとめ

今までの内容で、ループフィルターの設計で悩んでいた内容が解決されましたか？解決の糸口になったのであれば幸いです。

TI社のクロックIC製品は、クロックにまれるジッタを除去し、信頼性の高いシステムを構築するのに貢献します。しかし、そのICの性能を発揮されるには最適なループ帯域を見つけ出す必要があります。最適なループ帯域はシステム毎に変わるため、システム設計者は最適条件を自身で見出す必要があります。

同社から提供されるPCベースのアプリケーションソフト、PLLatimumを使うことで、容易に最適なループ帯域を見つけ、ループフィルターの部品定数を決定できます。

Texas Instruments社の製品をお探しの方は、メーカーページもぜひご覧ください。

Texas Instruments社
メーカーページはこちら

ノイズ源	伝達関数	ループ帯域より低い周波数領域 1<<G(s)	ループ帯域より高い周波数領域 1>>G(s)
VCO	$\begin{align} \frac{1}{1+G(s) \times H} \end{align}$	$\begin{align} \frac{1}{1+G(s) \times H} \fallingdotseq \frac {1}{G(s)} \times N \end{align}$	$\begin{align} \frac{1}{1+G(s) \times H} \fallingdotseq 1 \end{align}$
入力リファレンス	$\begin{align} \frac{1}{R \times CL(s)} \end{align}$	$\begin{align} \frac{1}{R} \times \frac {G(s)}{1+G(s) \times H} \fallingdotseq \frac{N}{R} \end{align}$	$\begin{align} \frac{1}{R} \times \frac{G(s)}{1+G(s) \times H} \fallingdotseq \frac{G(s)}{R} \end{align}$
入力分周器	CL(s)	$\begin{align} \frac {G(s)}{1+G(s) \times H} \fallingdotseq N \end{align}$	$\begin{align} \frac{G(s)}{1+G(s) \times H} \fallingdotseq G(s) \end{align}$
フィードバック分周器	CL(s)	$\begin{align} \frac{G(s)}{1+G(s) \times H} \fallingdotseq N \end{align}$	$\begin{align} \frac{G(s)}{1+G(s) \times H} \fallingdotseq G(s) \end{align}$
位相比較器	$\begin{align} \frac{1}{K \phi \times CL(s)} \end{align}$	$\begin{align} \frac{1}{K \phi}\times \frac{G(s)}{1+G(s) \times H} \fallingdotseq \frac {N}{K \phi} \end{align}$	$\begin{align} \frac{1}{K \phi}\times \frac{G(s)}{1+G(s) \times H} \fallingdotseq \frac {G(s)}{K \phi} \end{align}$

「PLLのループフィルターってどうやって決めるの？」気を付けるべき３つのポイント

はじめに

PLLの原理