公開日：2020年10月02日
| 更新日：2022年11月21日

PLLのループ帯域を決定する4つの要素とは？！

ライター：mtmt
クロック

「PLLのループフィルターってどうやって決めるの？」では、最適なPLLループ帯域とは何かについて触れました。下図に示す通り、ループ帯域が変われば、ロック時間は勿論のこと、位相比較周波数やそれに伴い量子化ノイズやスプリアス、最終的には位相ノイズに影響いたします。結果、出力ジッターに影響を及ぼします。最適なループ帯域の設定は位相ノイズとロック時間とのトレードオフで決まります。

ジッタークリーナやPLLの設計をしているときに、ループ帯域に影響する要素を考えたことはありませんか？当然ながら、支配的な部分はループフィルターです。本資料では、ループ帯域に影響を与える4つの要素を説明いたします。加えて、テキサスインスツルメンツ社（以下、TI社)提供のPLLシミュレーションソフト、PLLatimumを使い、これら4つの要素がループ帯域がどの様に影響するか検証しました。

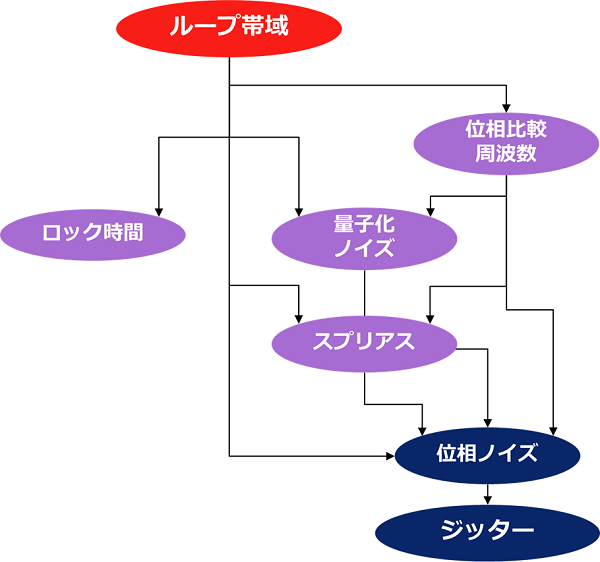
図.１　ループ帯域が与える影響について

ループ帯域を決定する4つの要素とは

ループ帯域に影響する要素は①ループフィルター, ②位相周波数比較器＋チャージポンプゲイン：KΦ, ③VCO利得：Kvco, ④分周器の4つです。(以下のPLLの図となります)それぞれについて簡単に触れます。

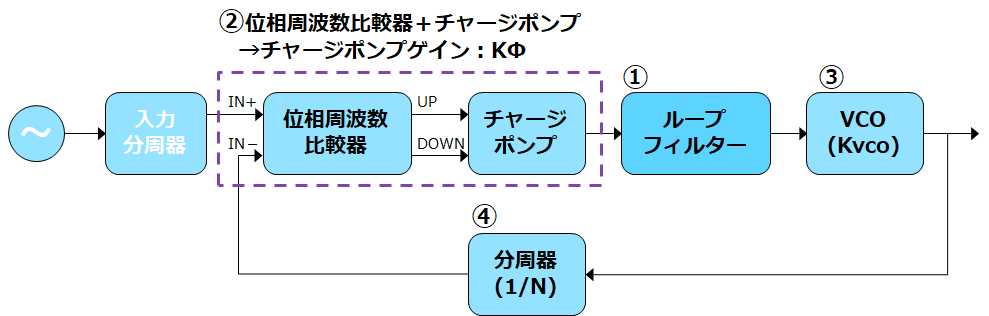
図.２　PLL 概略図

　ループフィルター
ループ帯域Fc(ループ利得=1になる周波数)を決定する支配的な要素です。フィルターの特性を変更するために使用します。

　チャージポンプのゲインKΦ
ループのゲインに影響を与えます。結果としてループ帯域に影響します。

　VCOゲインKvco
単位がMHz/Vを示す通り、入力した制御電圧に応じ出力周波数が変わります。チャージポンプのゲインKΦ同様、ループ帯域に影響します。

　分周器
VCOで変化する周波数は、分周器で１/Nになります。結果、ループ利得は１/Nになります。これらの結果をまとめると下式が導かれます。

$\begin{align*} \left K = \frac{K \Phi \times K_{vco}}{N} \end{align*}$

K：ゲイン
KΦ：チャージポンプゲイン
Kvco：VCOゲイン
N：分周比

ゲインKが変化すると、ループ帯域Fcがどう変わるか見てみます。
※ 各関係性における値の増減、拡大縮小を確認するため、スケーリング観点で説明を行います。

スケーリング視点

広く使われている二次ループフィルターの部品のスケーリングについて説明します。上記フィルター回路のインピーダンスは以下の式で求まります。

■計算内容■

$\begin{align*} \frac {1}{Z(f)} = \frac {1}{\frac {1}{\omega C1}} + \frac {1}{R2 + \frac {1}{\omega C2}} \end{align*}$

$\begin{align*} Z(f) = \frac {(R2 + \frac {1}{\omega C2}) \times \frac {1}{\omega C1}}{R2 + \frac {1}{\omega C2} + \frac {1}{\omega C1}} \end{align*}$

C1<<C2とすると、R2 <<1/ωC1, 1/ωC2<<1/ωC1が故、下式に近似できます

$\begin{align*} Z(f) \fallingdotseq \frac {(R2 + \frac {1}{\omega C2}) \times \frac {1}{\omega C1}}{\frac {1}{\omega C1}} \end{align*}$

ωに２πfを代入

$\begin{align*} Z(f) \fallingdotseq R2 + \frac {1}{2 \times \pi \times f \times C2} \end{align*}$

PLLのオープンループ利得G(s)は次式で示されます。

$\begin{align*} G(s) = \frac {K \Phi \times K{vco} \times Z(s)}{s} \end{align*}$

VCO利得は係数sで除算します。VCOの出力周波数を位相に戻すためです。虚数jの絶対値を取ると、以下になります。

$\begin{align*} |G(s)| = \frac {K \Phi \times K{vco} \times Z(s)}{s} \end{align*}$

上式にsにf、 K=Kφ・Kvco、Z(f)のそれぞれを代入すると以下になります。

$\begin{align*} G(f) = \frac {K \times Z(f)}{2 \pi f}= \frac {K \times( R2+ \frac{1}{2 \pi f \times C2})}{2 \pi f} \end{align*}$

ループ利得G(f)=1となるループ帯域Fcを求めると以下になります。

$\begin{align*} 2\pi F_c = K \times (R2 + \frac{1}{2 \pi F_c \times C2}) \end{align*}$

2πFcを両辺に掛けると以下になります。

$\begin{align*} (2\pi F_c)^2 = K \times 2 \pi F_c \times R2 + K \times \frac{1}{C2} \end{align*}$

上式を元に、Fc, R2, C2, Kのそれぞれの関係を抜き出すと以下になります。

■ループ帯域FcとR2との関係■

$\begin{align*} (2\pi F_c)^2 = K \times 2 \pi F_c \times R2 \end{align*}$

$\begin{align*} R2 = \frac{F_c}{K} \times 2 \pi \end{align*}$

$\begin{align*} F_c \propto R2 \times K \end{align*}$

■ループ帯域FcとC2、並びにKとの関係■

$\begin{align*} (2\pi F_c)^2 = K \times \frac{1}{C2} \end{align*}$

$\begin{align*} C2 = \frac {K}{F_c^2} \times \frac {1}{4 \pi ^2} \end{align*}$

$\begin{align*} F_C^2 \propto \frac {K}{c2} \end{align*}$

それぞれ上記の比例式から、何らかの理由でゲインKが2倍になった時、ループ帯域を同じに保つには、抵抗R2を1/2にすることになります。コンデンサは√2倍にします。
※4倍でも理屈は同じです。抵抗は1/4に、コンデンサは2倍にします

上記のことから、R2とCの値, K(チャージポンプゲインKΦ、VCOゲインKvco、分周器N)がループ帯域Fcに関わることがわかりました。

PLLatinum(シミュレーション)を用いて実際のループ帯域が変化するかの確認

では実際にPLLatinumを使ったシミュレーションでループ帯域の変化をみてみます。（例として、TI社製品のLMK03328で2次ループフィルターを使用して、各条件でシミュレーションいたします。)

　■変更前の設定■

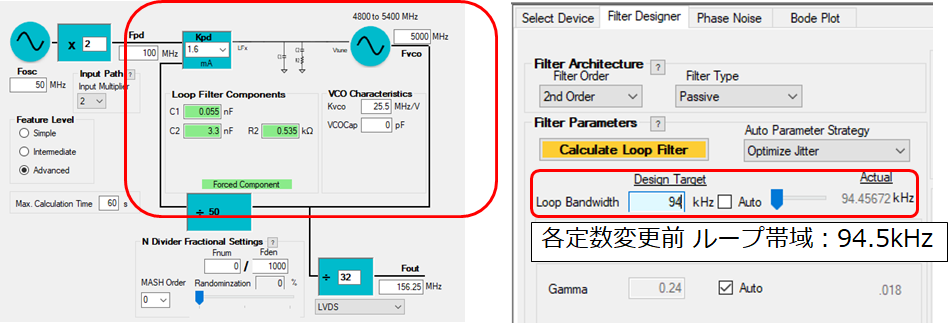
図.３　PLLatinum(変更前設定)画面

→NとループゲインKが反比例します(N上昇に伴い、ループ帯域値が減少)

■チャージポンプゲインKΦ 1.6mA→6.4mAに変更■

図.４　PLLatinum(チャージポンプ変更)画面

→KΦとループゲインKが比例します(KΦ上昇に伴い、ループ帯域値が増大)

■VCOゲインKVCO 25.5MHz/V→51MHz/Vに変更■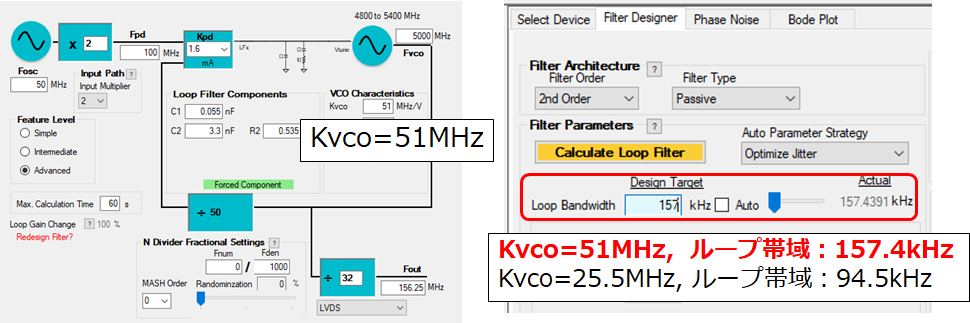

図.５　PLLatinum(VCO変更)画面

→KvcoとループゲインKが比例します(Kvco上昇に伴い、ループ帯域値が増大)

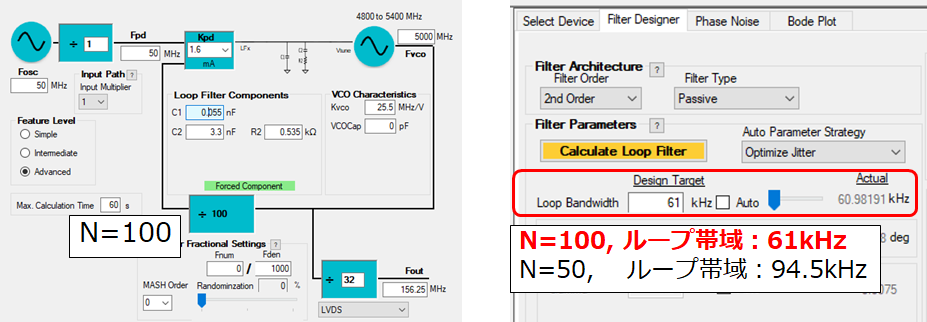
　■分周比N 50→100に変更■

図.６　PLLatinum(分周比変更)画面

→NとループゲインKが反比例します(N上昇に伴い、ループ帯域値が減少)

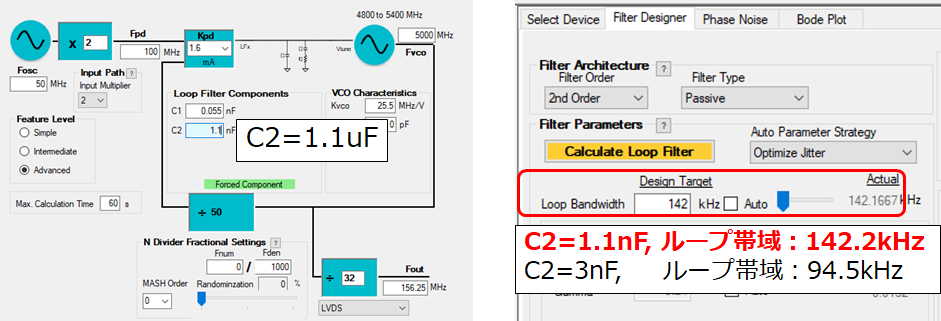
　■定数Cの変更 C2=3.3nF→1.1nF ■

図.７　PLLatinum(定数C変更)画面

→ループ帯域とコンデンサCが反比例関係のため、C2値下降でループ帯域値が増大します

　■定数Rの変更 R2=0.535kΩ→3.099kΩ■

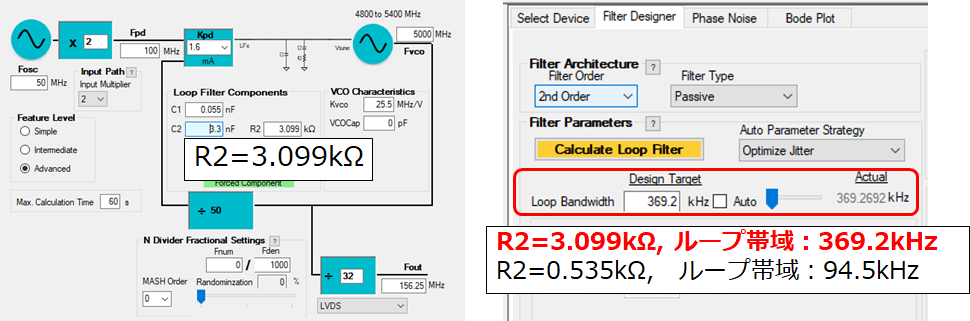
図.８　PLLatinum(定数R変更)画面

→ループ帯域と抵抗Rが比例関係のためR2上昇でループ帯域値が増大します

前章「スケーリング視点」で説明した通り、ループフィルターの各要素、R2, C2, ゲインKがどの様にループ帯域に影響するか、シミュレーションで確認できました。

※ この資料ではループフィルターの各要素、R2, C2, ゲインK がどの様にループ帯域に影響を及ぼすかについてのみ議論しました。最適なループフィルターを設計するには、ループ帯域に加え、安定的にPLLを動作を動作させるため、位相余裕を検証する必要があります。

まとめ

ループ帯域を決める要素が何か、今まで疑問だった内容は解決されましたでしょうか？本資料にて、解決のヒントになれば幸いです。

クロックICを使用して設計する際に重要なことは、クロックに含まれるジッターを除去することです。加えて、ロック時間とのトレードオフも考慮が必要です。ICが持つ最大限の性能を発揮されるには最適なループ帯域を見つける必要があります。ループ帯域を決定する支配的な内容は、当然ながら、ループフィルターになります。しかしながら、ループフィルターの部品定数に加え、ＶCOゲイン, チャージポンプゲイン,分周器がループ帯域に影響を及ぼすことを知る必要があります。

システム設計者は、これら要素の影響を踏まえて最適条件を見出すことが必要です。シミュレーションソフトPLLatinumを使用することで、複雑な計算式から解放され、希望するループ帯域を実現するためのフィルター部品定数を見つけ出すことができます。

是非有効活用し、最適な設計をしていただければ幸いです。

お問い合わせはこちらから！