拡張ハミング符号の仕組み　誤り検出・訂正基礎講座 第3回

はじめに

前回の記事ではハミング符号について解説しました。ハミング符号は1bitのエラー訂正を行えましたが、2bit以上のエラーになると、エラー検出を正しく行えませんでした。今回は2bit以上のエラーが出力されたときにもエラー検出を行うことが可能な、拡張ハミング符号について解説します。まだ前回の記事を読んだことがない方は、そちらの記事をご覧いただいた後にこちらの記事を読むと理解しやすいと思います。

前回の記事：ハミング符号の大枠を掴もう　誤り検出・訂正基礎講座  第2回

拡張ハミング符号

ハミング符号は1bitのエラー訂正が可能なもので、情報ビットと符号ビットで構成されるものでした。ハミング符号は、2bit以上のエラーは訂正も検出もできないという問題がありましたが、このハミング符号を拡張し、1bitのエラー訂正と、２bitのエラー検出を可能にしたものを拡張ハミング符号と呼びます。ハミング符号に2bitのエラー検出の機能を追加するのは非常に簡単で、ハミング符号に1bitのパリティビットを追加するだけで実現できます。[1010]のデータを拡張ハミング符号にエンコードして送信する例を見てみます。

拡張ハミング符号のエンコード

エンコードはハミング符号と同様に、データ(情報ビット) ”1010” とエンコード用の行列の積から、符号ビット ”010” を求めます。そして、得られたハミング符号(情報ビット+符号ビット) ” 1010010”のパリティビットを求めます。上の例ではパリティビットは”1”です。このエンコードで得られた ”101000101” を使ってデータをデコードし、1bitのエラー訂正と2bitのエラー検出を行います。

拡張ハミング符号のエラー訂正とエラー検出

では、例を参考にどのように2bitのエラー検出を行うのかみてみましょう。

拡張ハミング符号のデコード(エラー無し)

デコードはハミング符号と同様の手順で行います。デコード時にはパリティビットを含めず演算し、XORの結果を求めます。そして次に、パリティビットを含めた10100101bを1bit単位でXORしパリティチェックを行います。結果が0(つまり1の数が偶数)ならパリティエラーは無しとなります。

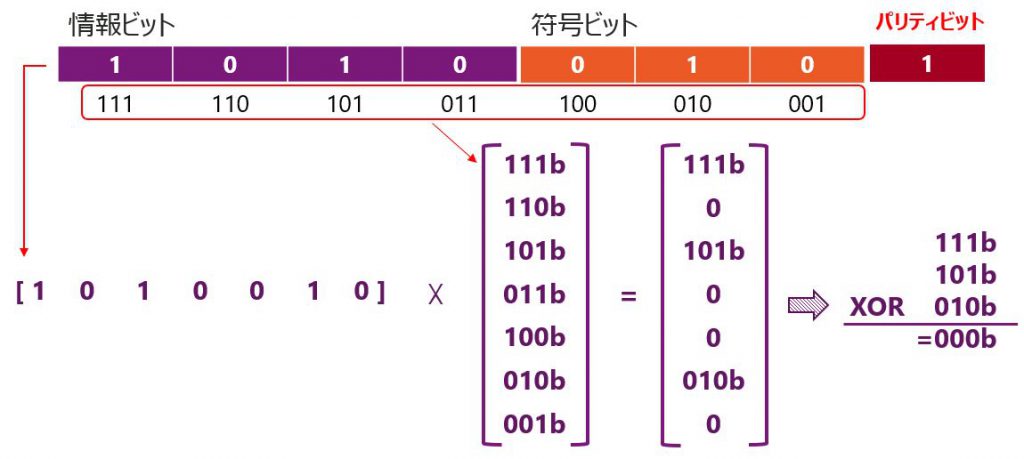
エラーの無いとき拡張ハミング符号の結果は以下のようにとなります。

• デコード結果(XOR)は0
• パリティエラー無し

拡張ハミング符号のデコード(1bitのビット化け発生時)

情報ビットに1bitのビット化けが発生した場合を見てみます。

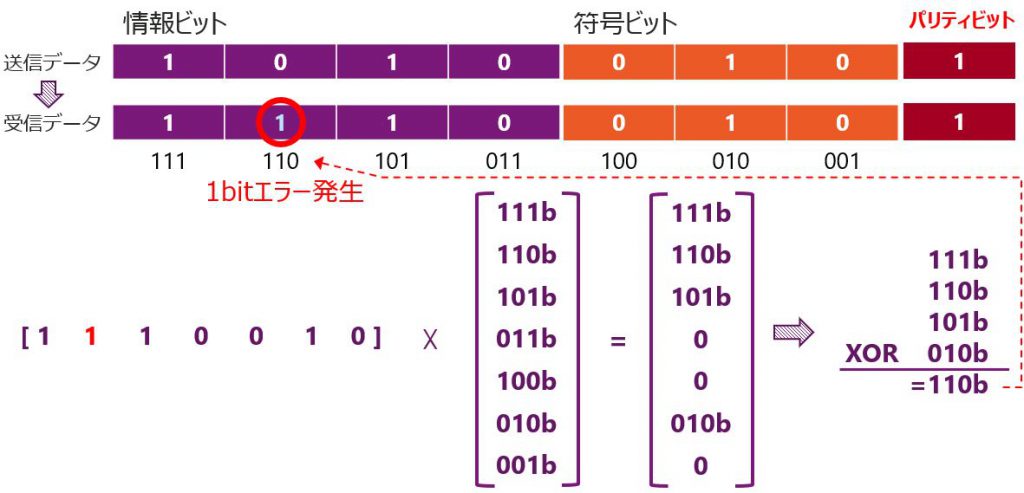
1bitエラーが発生したときの拡張ハミング符号の結果は以下のようにとなります。

• デコード結果(XOR)はビットエラーが発生した箇所を示す。(110b)
• パリティエラー有り

パリティエラーについては、受信データの”11100101″のパリティチェックを行い、エラー判別します。
今回は”1″の個数が奇数個になっているのでパリティエラーとなります。

拡張ハミング符号のデコード(2bitのビット化け発生時)

情報ビットに2bitのビット化けが発生した場合を見てみます。

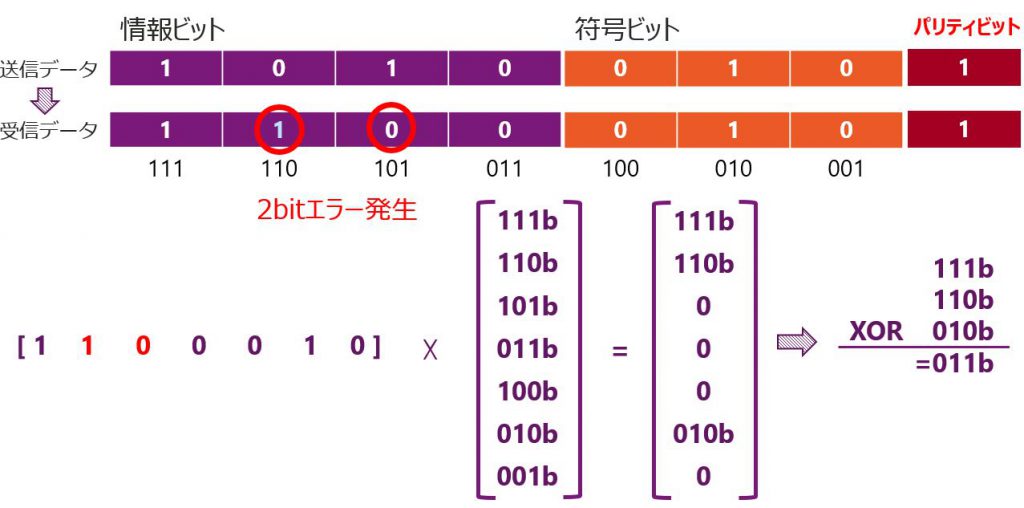
2bitエラーが発生したときの拡張ハミング符号の結果は以下のようにとなります。

• デコード結果(XOR)は0以外の値となる
• パリティエラー無し

パリティエラーについては、受信データの”11000101″のパリティチェックを行います。2bitのデータが反転しているので、
今回は”1″の個数が偶数個になりパリティエラーは無しとなります。

これらのデコード結果とパリティチェックの結果の組み合わせで、エラー無し、1bitエラー訂正、2bitエラー検出が可能となります。

	デコード結果	パリティチェック
エラー無し	0	エラー無し
1ビットエラー	エラー箇所を示す	エラー有り
2ビットエラー	0以外の値を出力	エラー無し

 

この結果からハミング符号に1bitのパリティビットを付与することで、1bitのエラー訂正と、2bitのエラー検知が可能になることがわかりました。ただし、3bit以上のエラーが発生した場合には、エラーの検出は不可能となっています。

拡張ハミング符号の行列演算

ここまでハミング符号の原理について説明しましたが、上で説明した方法の場合、デコードの計算と、パリティチェックの2種類の演算をする必要があります。この計算を一つの行列演算にまとめる方法があるので、その方法についてここで解説します。

拡張ハミング符号の行列演算によるデコード(エラー無し)

デコードの際に使用するシンドロームテーブルを少し修正することで、デコードの計算と、パリティチェックを一つの行列演算で求めることができます。シンドロームテーブルには、先程のテーブルの一番下の行に”0”を追加します。そして、一番右の列に”1”を追加します。このシンドロームテーブルを用いると、パリティを含めたビット列を用いて計算が可能になります。このシンドロームテーブルとパリティを含めたデータを掛け算し、その結果をXORしてデコードします。

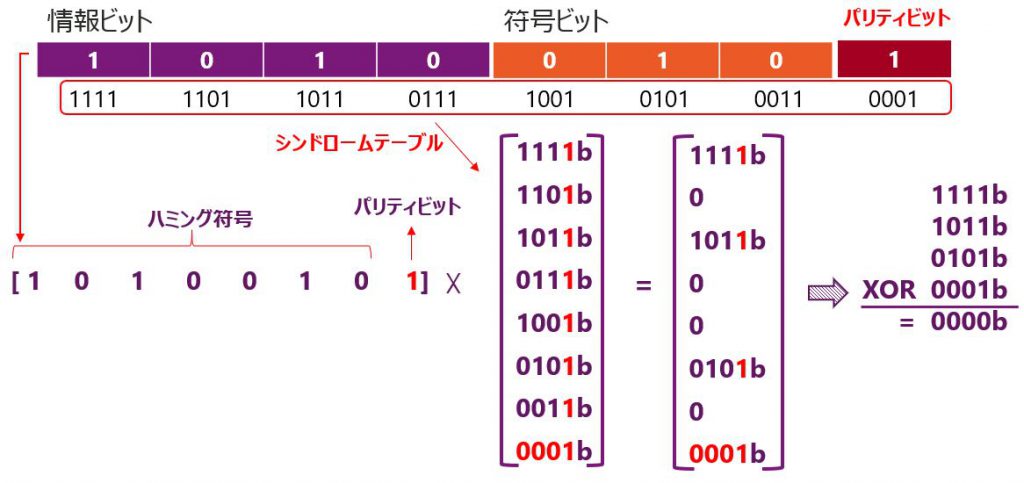
エラーが無いときの拡張ハミング符号の行列結果は以下のようにとなります。

• デコード結果(XOR)は0

拡張ハミング符号の行列演算によるデコード(1bitのビット化け発生時)

情報ビットに1bitのビット化けが発生した場合を見てみます。

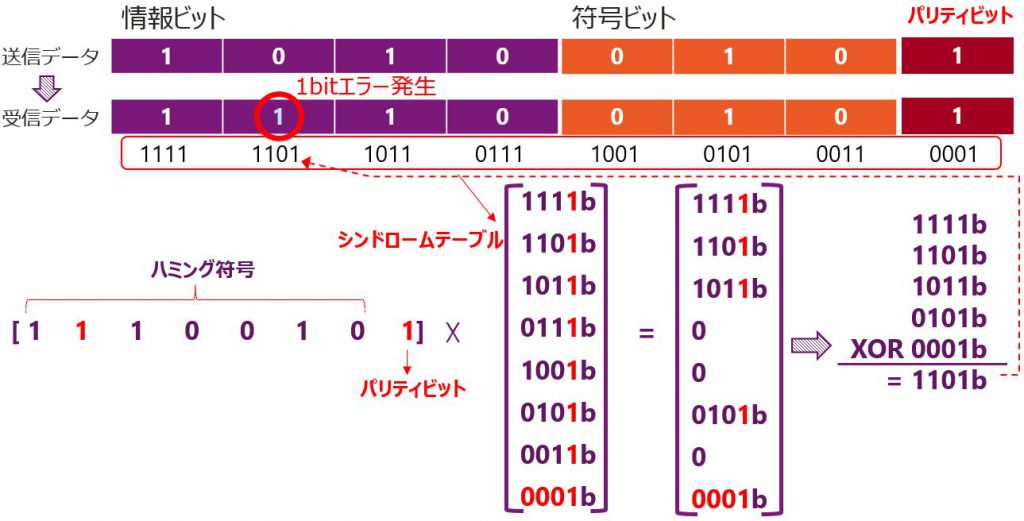
1bitエラーが発生したときの拡張ハミング符号の行列演算結果は以下のようにとなります。

• デコード結果(XOR)はビットエラーが発生した箇所を示す。(1101b)

拡張ハミング符号の行列演算によるデコード(2bitのビット化け発生時)

情報ビットに2bitのビット化けが発生した場合を見てみます。

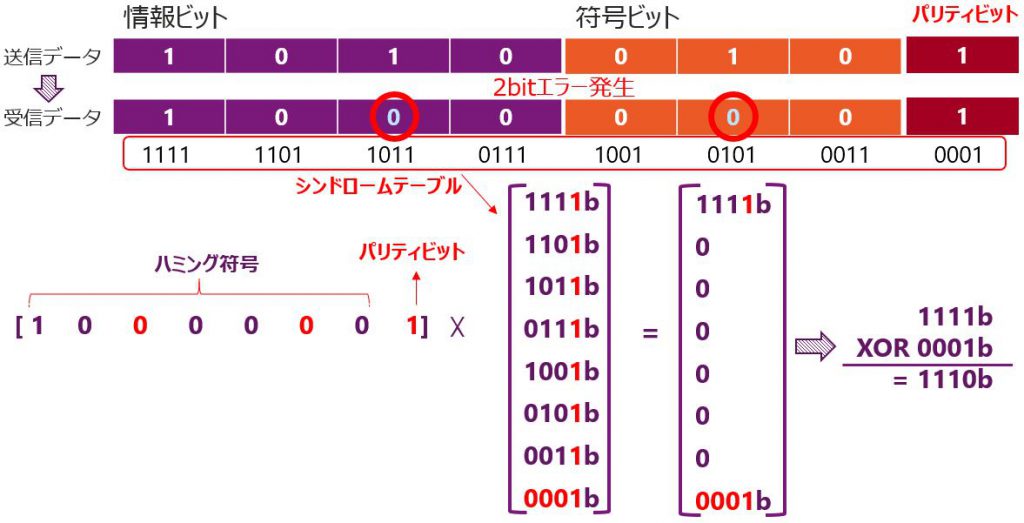
2bitエラーが発生したときの拡張ハミング符号の行列演算結果は以下のようにとなります。

• デコード結果(XOR)はシンドロームテーブルに無い値となる

この行列演算でのデコードでエラー無し、1bitエラー訂正、2bitエラー検出が可能となります。なぜこのようになるかというと、シンドロームテーブルの一番右のビットがパリティチェックの計算になっており、0ならばパリティエラー無しとなります。そのためエラーが無いときはデコード結果が0になり、1bitエラーのときは一番右のビットが1となり、エラーの該当箇所を示します。2bitエラーのときは、一番右のビットが０となり、パリティエラーは無しとなりますが、シンドロームテーブルの一番右は全て1で構成されており、該当の箇所が存在しないため、受信データにエラーがあると判断ができるようになります。

さいごに

今回は拡張ハミング符号の仕組みについて説明しました。1bitのエラー訂正が可能なハミング符号に、1bitのパリティビットを追加することで、2bitの誤り検出まで行えることがわかりました。今回の例では4bitの情報ビットと3bitの符号ビットを使い、視覚的に理解しやすいように解説しましたが、実際にメモリのエラー訂正・検出を行うときには、情報ビットを64bit、128bitなど、もっと大きなサイズで扱うことが多いです。ただ、いくらサイズが大きくなってもやっていることは同じなので、こちらの記事を参考に実際に使用しているメモリやマイコンのECC機能の確認をしてみてください。実際の製品を用いて確認、計算をしてみるとより理解が深まると思います。