わかりやすいPID制御

はじめに

この記事では、モーター制御などでよく用いられるフィードバック制御のひとつであるPID制御について解説します。PID制御は入力値を目標値と比較して、出力値を制御するものになりますが、初めてこの制御を使う方は、使い方のイメージがし難いと思います。そこでこの記事では、初めての方でも理解できるように、使用例を見ながら、具体的にどのように制御を行っているのか確認していきます。PID制御は、P制御(Proportional)、I制御(Integral)、D制御(Differential)を組み合わせたものになりますので、それぞれの制御の特徴を一つずつ確認していきます。

P制御

最初にP制御について解説します。名前のとおり比例(Proportional)制御になるので、目標値との差に比例して出力値を制御します。以下のモーター制御を例にすると、モーターの位置情報などを入力値とし、目標値との差分から出力値を算出します。

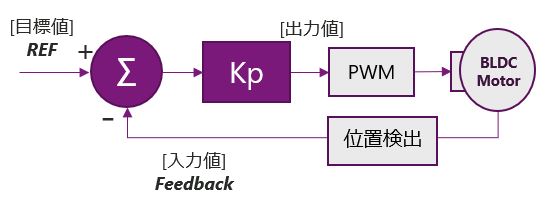
P制御の比例ゲインであるKpが大きいほど出力値が目標値に近づく時間が早くなります。下の図を例にすると、目標値と入力値の差が大きいときは、早く目標値に近づけようと、グラフの傾きが急になりますが、目標値に近づくにつれて、傾きは緩やかになっていきます。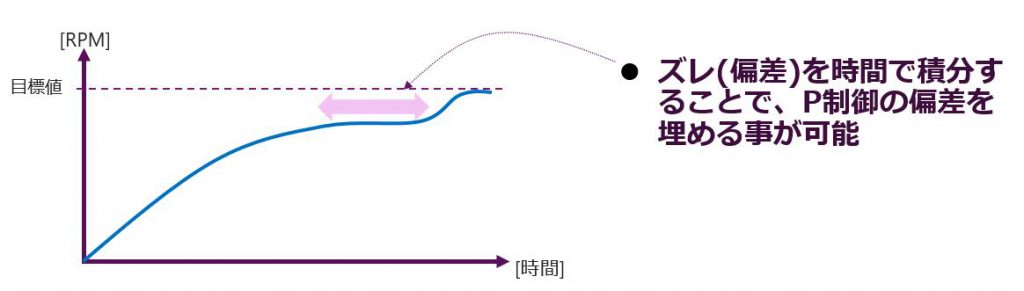

 

このP制御は比例制御なので、下の式のように、指令値と実速度の差にKpを掛けたものを出力します。とてもシンプルにプログラムに実装できます。

Vp = (REF – Feedback) x Kp

ただし、P制御の問題点としては、目標値に近づくと安定し、目標値と出力値に偏差(ズレ)が生じてしまうということです。では具体的な例を用いてもう少しこのP制御の偏差について見てみたいと思います。下のヘリコプターを100mの高さまで飛ばすことを考えます。制御は位置制御が必要になるので、目標値と入力値は高さで制御を行います。この制御に２つの条件を用意します。

条件

• 制御の出力は、”位置の差分”に”Kp”をかけたものをRPMにして出力
• ホバリングするには200RPMが必要

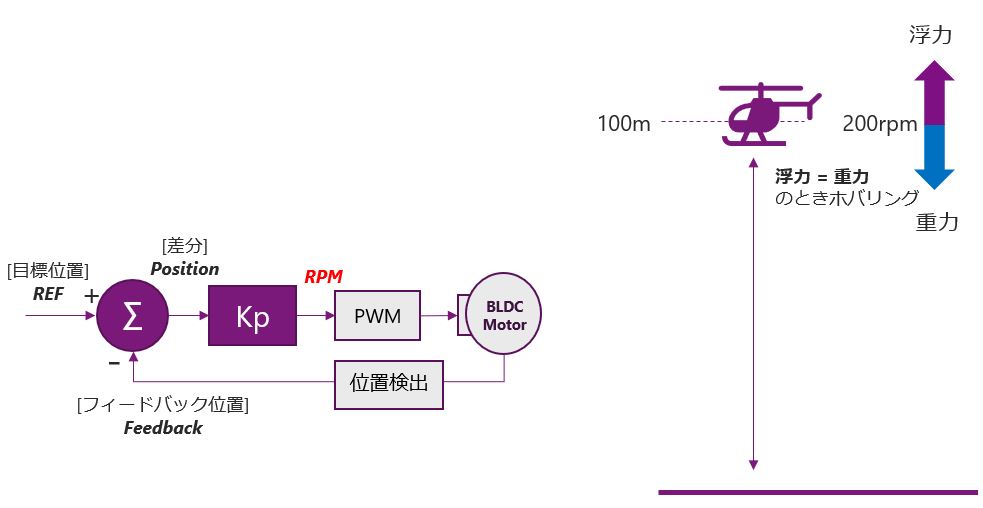
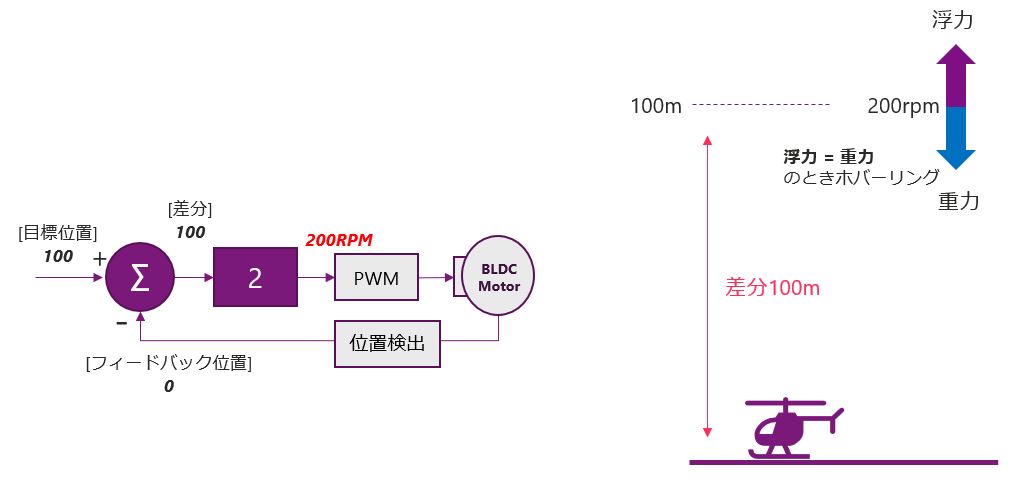
このヘリコプターの例を使い、Kpの値により動作がどのように変わるか確認していきます。まずはじめに、下の図のように目標位置を100m、Kp=2の場合を見てみます。ヘリコプターは最初、地上に存在するので、100-0で、差分は100になります。この100にKpの2をかけると200RPMとなります。200RPMはホバリングする回転数なので、ヘリコプターは高さ0mでホバリングをします。その場でホバリングをし続けるだけなので、当然次の制御ループのフィードバック位置も0mになり、このシステムでは、高さ0mでヘリコプターは安定してしまいます。

 

続いてKp=5の場合を見てみます。ヘリコプターは最初、地上に存在するので、100-0で、差分は100になります。この100にKpの5をかけると500RPMとなりますので、ヘリコプターは上昇をします。次の制御ループのフィードバック位置も0mよりも高い位置になるので、差分は100より小さくなります。

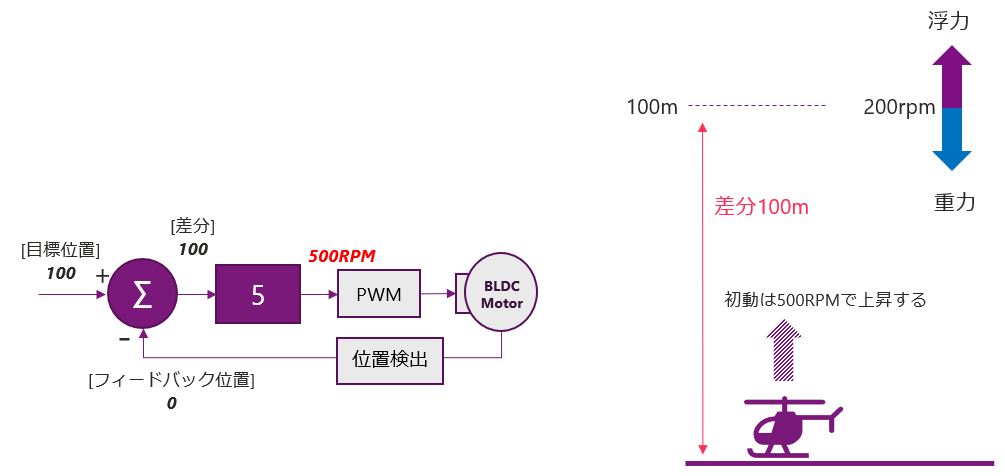
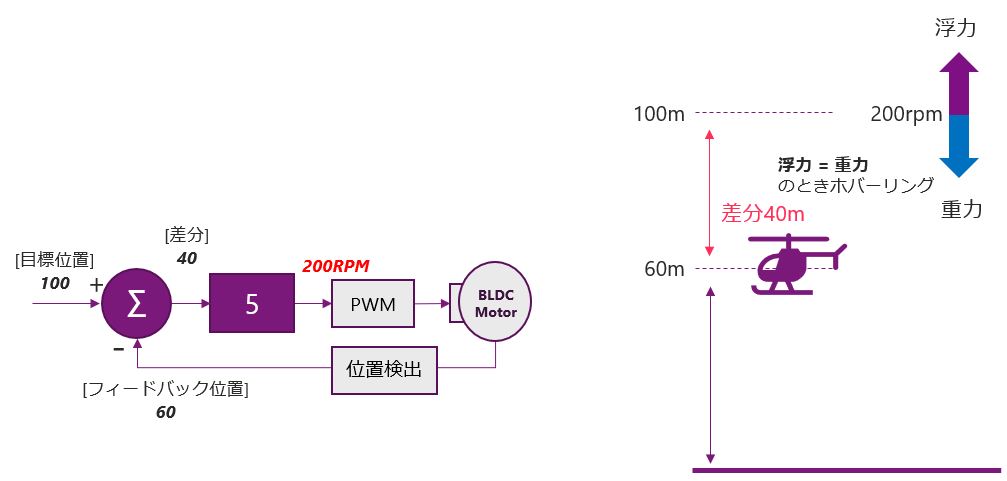
そして時間が経ち、差分は100より小さくなり、フィードバック位置が60mになったときにこのシステムは安定します。下の図のように100-60で差分は40。これにKpの5をかけることで200RPM。つまり、高さ60m地点で、ヘリコプターは安定することになります。先程のKpが2のときよりは目標値に近づきましたが、まだ目標値との間には差分があります。

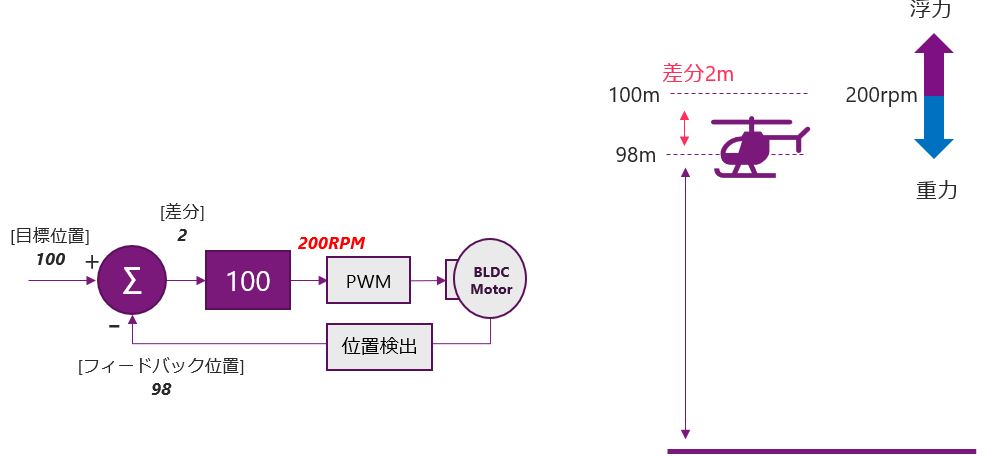
最後にKpが100の時を考えてみます。ヘリコプターは最初、地上に存在するので、100-0で先ほどと同様に、差分は100になります。この100にKpの100をかけると10000RPMとなりますので、ヘリコプターは急上昇をします。このシステムでも最終的には高さ98mで安定します。100-98で差分は2になり、Kpの100をかけることで、ヘリコプターはホバリング状態となります。つまり、Kpをいくら大きくしてもこの誤差は消えない！ということになります。またKpを極端に大きくしすぎると、モーターが追従できずにシステムとして動作しなくなる場合もあります。この誤差を埋めるための制御としてI制御、積分制御があります。

PI制御

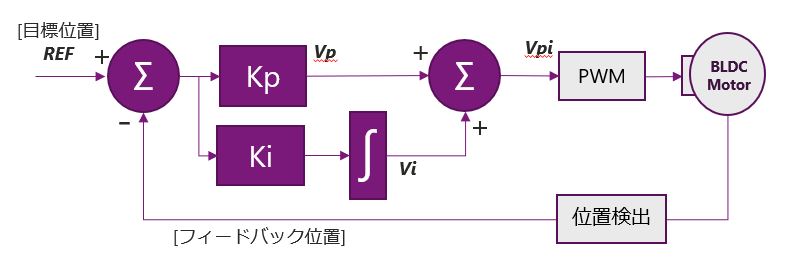
I制御では、偏差を時間で積分することで、P制御の偏差を埋めます。システムブロック図としては今回はKpと並列にKiを接続します。

では具体例でこのI制御を見ていきたいと思います。

先程と同様にヘリコプターの例を用います。条件は先ほどと同様に200RPMでホバリングするヘリコプターとします。先程のP制御のみだと、Kpが100のとき、偏差は2mとなり、高さ98mで安定しました。ここにI制御が加わると、下の図の左のErrorの青線グラフが積分されます。これが出力に加えられますので、200RPmよりも高いRPMが出力され、さらにヘリコプターは上昇できるようになります。

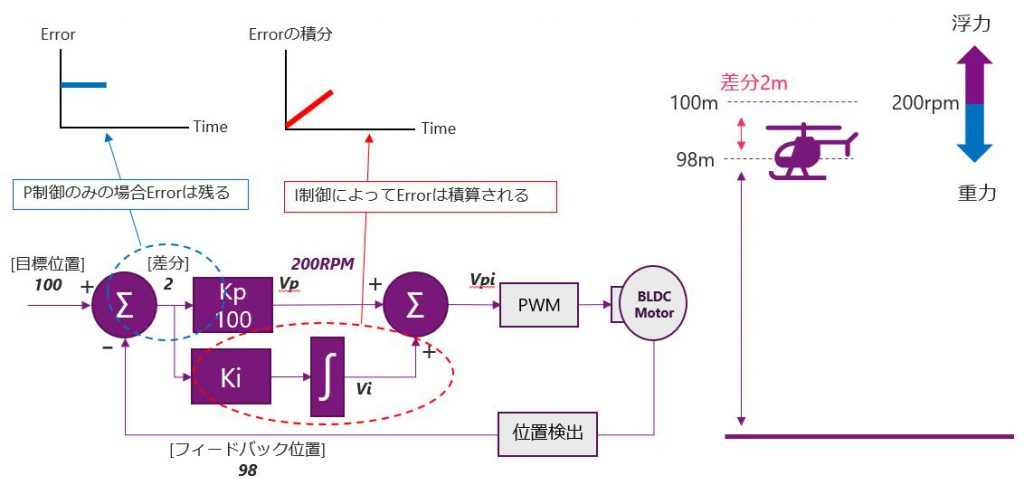
Errorの積分により、差分が縮まり、この差分が1mになると、下の図のように左の青線グラフの高さも低くなりますので、積分の出力はさらに緩やかになりますが、引き続き目標の位置に近づきます。

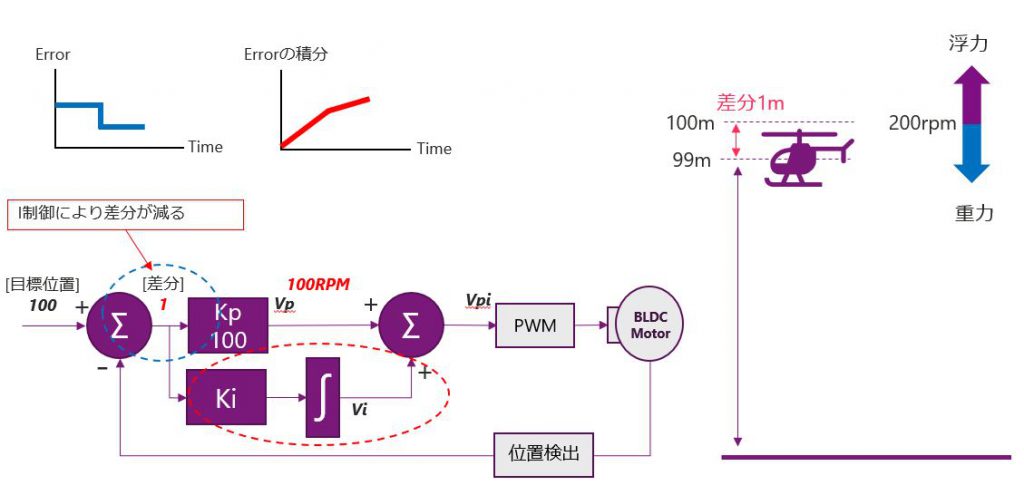
最終的には、差分が0になり、その状態でヘリコプターはホバリングを続けるような動作となります。このPI制御で、システムは目標値に到達できるようになります。

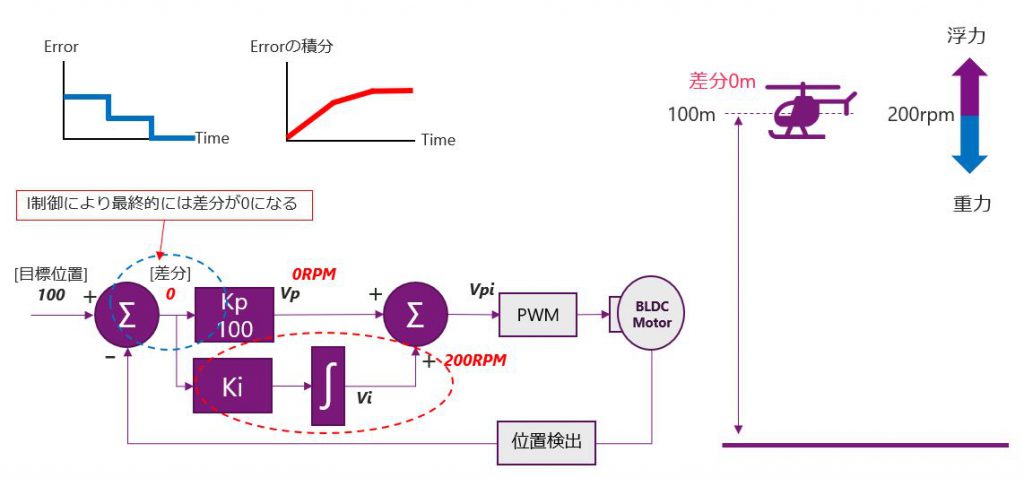
PID制御

では最後にPID制御を見てみます。先ほどのPI制御で目標値に達することができましたが、実際にはPI制御のみだとオーバーシュートが発生することがあります。目標値に高速に近づけるために、Pを大きくしすぎると、このオーバーシュートは発生しやすくなります。このオーバーシュートを抑えるために、コントローラに負成分を追加します。この負成分が、D制御(微分制御)になります。この微分制御をPとIと並列に組み込んだ例を見てみます。

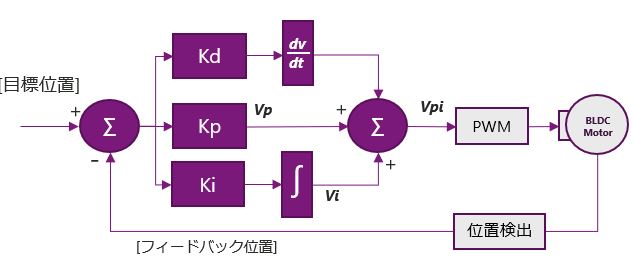
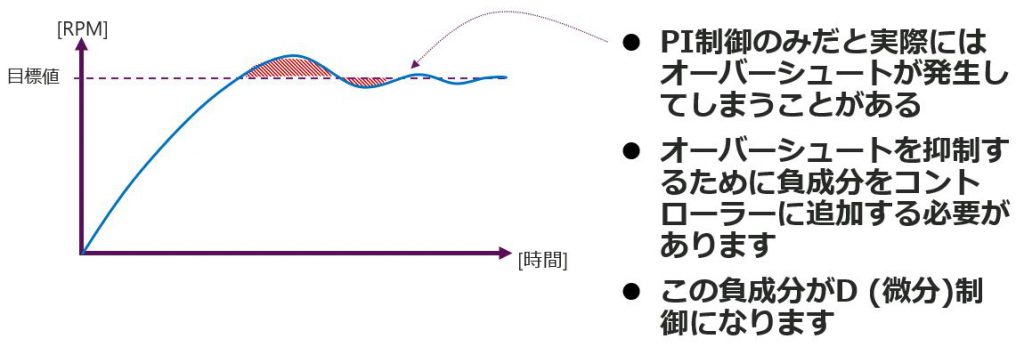
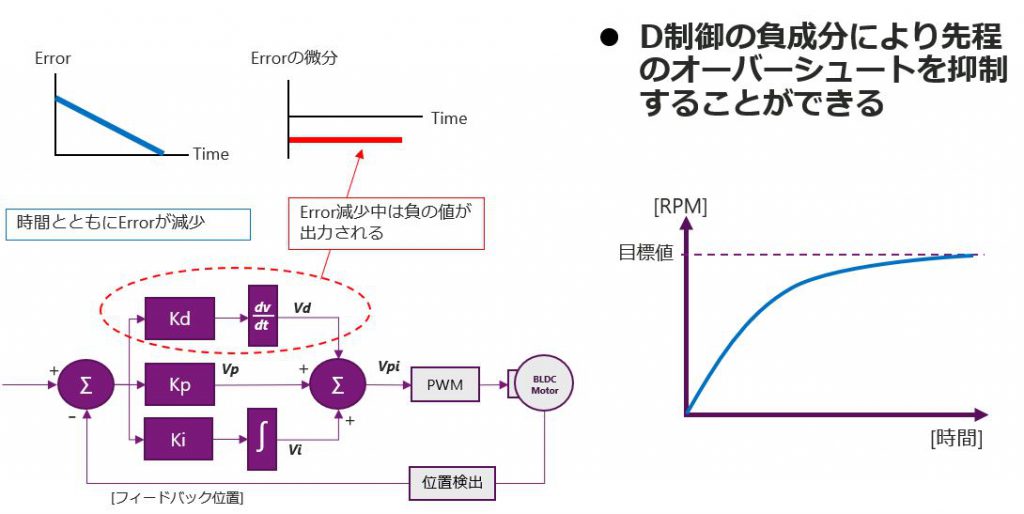
先程のPI制御では、時間とともに、Errorは減るので、左のグラフのような右肩下がりのErrorとなります。D制御でこのErrorを微分するので、出力は負の値が出力されます。つまり、急速にErrorが減るほど負成分は強く働きます。このP、I、Dの３つの制御の組み合わせから最適な、Kp、Ki、Kdを設定し、安定して素早く目標値に達するシステムを構築することができます。

PID制御のC言語プログラム例

PID制御はマイコンのプログラムで実装することが多いと思いますが、プログラムは非常にシンプルになっており、以下のように記述することで実現できます。

float pid_culc(float feedback_val, float target_val)
{

float p, i, d;

error[0] = error[1];
error[1] = feedback_val – target_val;
integral += (error[1] + error[0]) / 2.0 * DELTA_T;

p = KP * error[1];
I = KI * integral;
d = KD * (error[1] – error[0])/DEDLTA_T;

return (p + i + d);

}

error[1]は現在のエラー値、error[0]は1つ前のエラー値になります。P制御は現在のエラー値error[1]とKpの積から出力値を求めます。I制御は縦軸をError値、横軸を時間にし、このerror[0]とerror[1]から時間の積分(面積)を求めます。DELTA_Tはerror[0]とerror[1]の間の時間になります。D制御も縦軸をError値、横軸を時間にしerror[0]とerror[1]から微分(グラフの傾き)を求めまています。

さいごに

今回はPID制御について、例を参考に動作について確認してみました。このように、一つの例で理解すると、非常にシンプルな制御であることが分かると思います。今回の例では目標値とフィードバック値を”位置”にして制御を行いましたが、モーター制御では、この目標値とフィードバック値を、”速度”や”電流”で制御をすることもあります。値が何であれ、制御で行うことは今回の例で行っていることと同様です。そしてユーザーにてとって、このPID制御で最も大事なことは、システムに最適なP、I、Dの値を設定することです。ユーザーはカットアンドトライなどで、この３つのパラメータを設定したり、ツールメーカーから提供されているシミュレータなどを使って調整を行い、システムに最適なPIDパラメータを求め、それを使い制御を行います。

ルネサス製品をお探しの方はぜひメーカーページもご覧ください。

ルネサス
メーカーページはこちら