BCH符号とは 誤り検出・訂正基礎講座 第4回

はじめに

前回の記事では拡張ハミング符号について解説しました。拡張ハミング符号は1bitのエラー訂正と2bitのエラー検出が行えましたが、3bit以上のエラーになると、エラー検出を正しく行えませんでした。今回は複数ビットのエラーが出力されたときにもエラー訂正・検出を行うことが可能な、BCH符号について解説します。まだ前回の記事を読んだことがない方は、そちらの記事をご覧いただいた後にこちらの記事を読むと理解しやすいと思います。

前回の記事：誰でも直ぐに分かる！誤り検出・訂正基礎講座③ 拡張ハミング符

BCH符号

BCH符号はハミング符号の符号ビットを増やし、エラー訂正可能なビット数を増やしたものになります。言い換えると、BCH符号の中で1bitのエラー訂正可能なものがハミング符号になります。
また、メモリコントローラーなどにBCH符号の機能が入っている場合、t=4、t=8、t=16などと書かれているのをよく見ると思いますが、このtはエラー訂正可能なビット数を表します。tが大きいほどエラー訂正可能なビット数は増えますが、それにともない符号ビットも増えます。
まず、[1010000]のデータをBCH符号でエンコードして送信する例を見てみます。

BCH符号のエンコード

まず、(15,7)BCH符号のエンコードの例を見てます。この例では2bitのエラー訂正が可能になります。
※(15,7)は情報ビットが7bit、符号ビットが8bitで表されるトータル15bitのBCH符号になります。

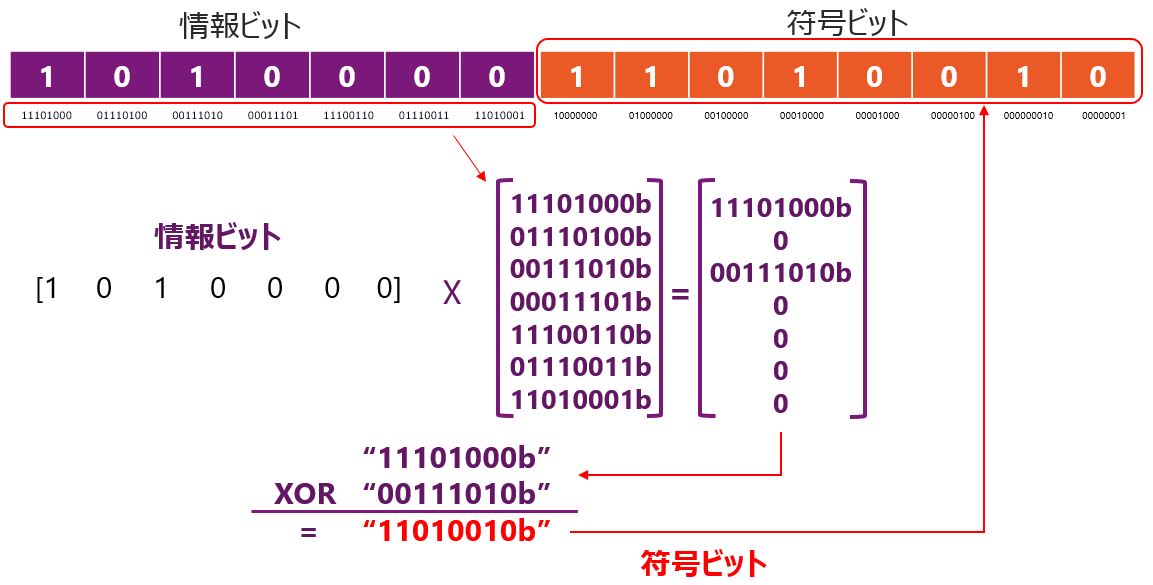
エンコードはハミング符号と同様に、データ(情報ビット) ”1010000” とエンコード用の行列の積から得られた値をXORし、符号ビット ”11010010” を求めます。ご覧いただくと、やっていることはハミング符号と全く同じになり、異なるのはエンコード用の行列と、符号ビットのビット数のみになります。

BCH符号のエラー訂正とエラー検出

では、例を参考にどのように2bitのエラー訂正を行うのかみてみましょう。

(15,7)BCH符号のデコード(エラー無し)

デコードはハミング符号と同様の手順で行います。15bitのデータ(情報ビット＋符号ビット)とシンドロームテーブルの積を求め、その結果をXORしてエラーを判別します。結果が0であればエラーは無しとなります。

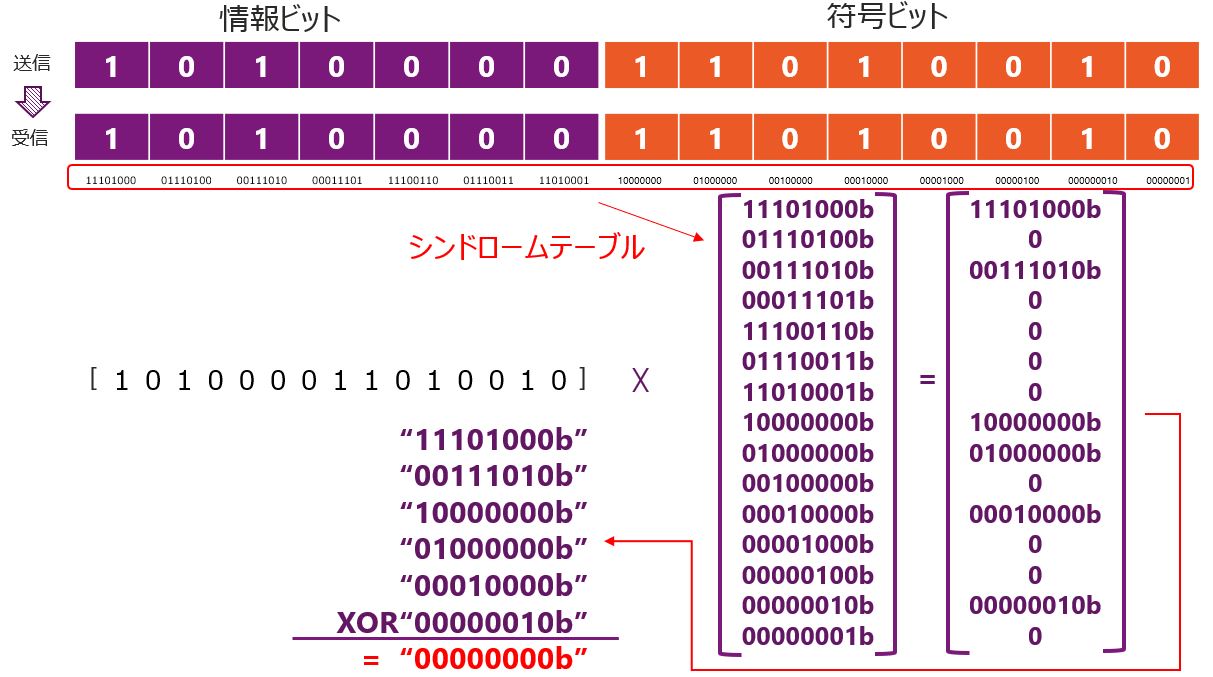
(15,7)BCH符号のデコード(1bitのビット化け発生時)

情報ビットに1bitのビット化けが発生した場合を見てみます。

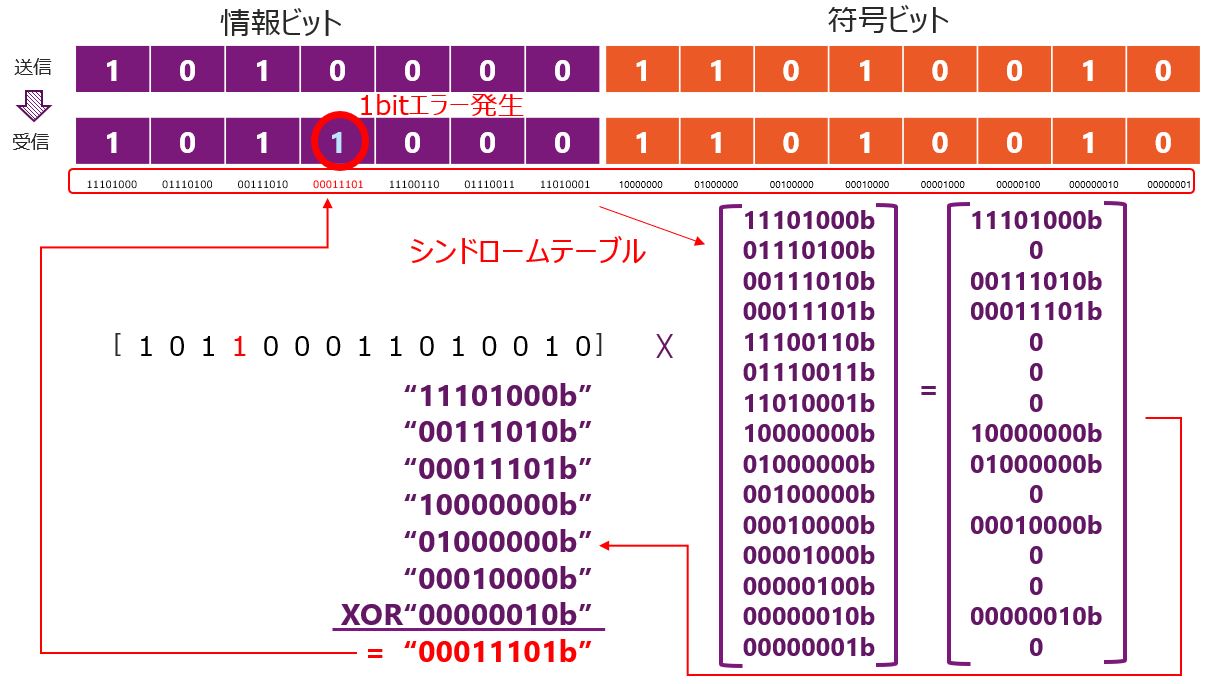
ハミング符号と同様に、１bitのエラー発生時には、デコード結果(XOR)はビットエラーが発生した箇所(00011101)を示します。

(15,7)BCH符号のデコード(2bitのビット化け発生時)

情報ビットに2bitのビット化けが発生した場合を見てみます。

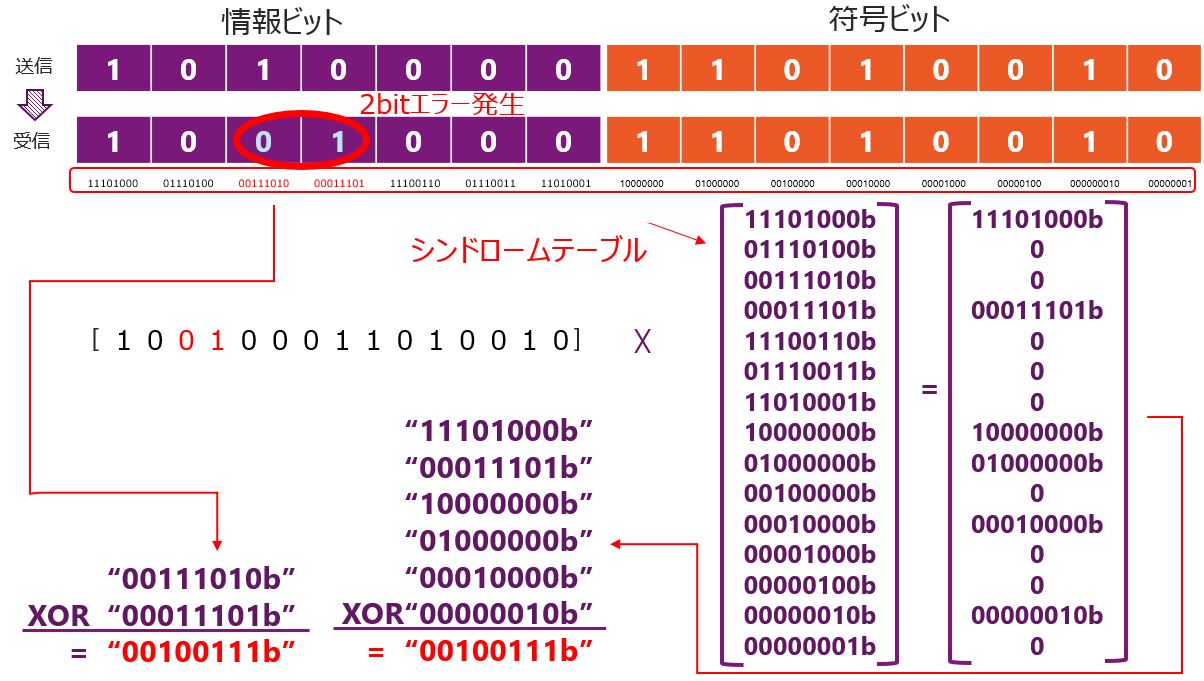
2bitエラーの場合には、シンドロームテーブルに無い値が出力されます。そして2bitエラーのときには15bitの中の特定の2bitのXOR値が出力されます。今回の例では”00100111″が出力されましたが、これは2bitのエラーが発生したビットの”00111010″と”00011101″をXORした値になります。そのため、この2bitが誤っているとデータであると判別できます。ただし2bitのエラーの場合、即座にどの2bitがエラーになっているかは判断ができませんので、基本的には予めROM内に2bitエラーの全てのパターンを登録しておき、それを参照して2bitエラーの場所を知ります。

このように、BCH符号は符号ビットとシンドロームテーブルのビット数を増やすことで、2bitエラー時の出力結果が全て独立した値になるように調整されています。この(15,7)BCH符号の場合には、2bitまでのエラー訂正しかできません。3bit以上のエラー訂正をする場合には、さらに符号ビットとシンドロームテーブルのビット数を増やす必要があります。

(15,5)BCH符号のデコード(3bitのビット化け発生時)

最後に(15,5)BCH符号を見てみます。先程よりも符号ビットとシンドロームテーブルのビット数が増えており、3bitまでのエラー訂正が可能になります。

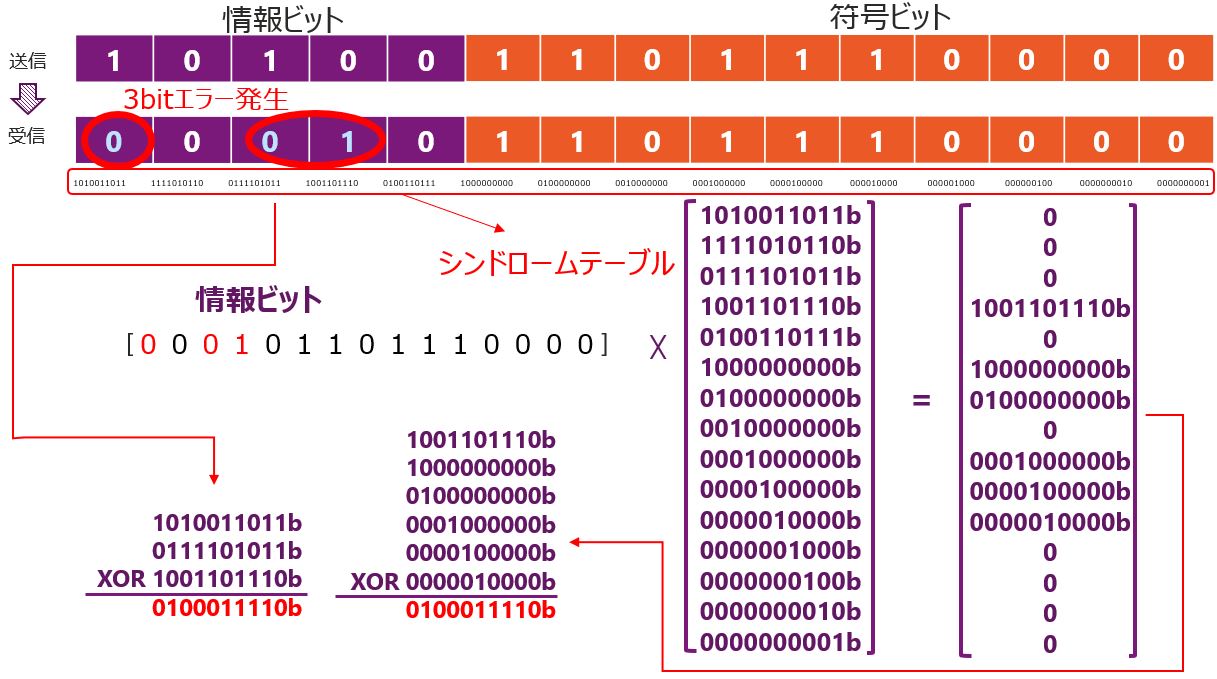
今回の場合も2bitエラーのときと同様に、シンドロームテーブルに無い値が出力されます。そして3bitエラーのときには15bitの中の特定の3bitのXOR値が出力されます。今回の例では”0100011110″が出力されましたが、これは3bitのエラーが発生したビットの”1010011011″と”0111101011″と”1001101110″をXORした値になります。そのため、この3bitが誤っているとデータであると判別できます。こちらも同様に、基本的には予めROM内に3bitエラーの全てのパターンを登録しておき、それを参照して3bitエラーの場所を知ります。

さいごに

今回はBCH符号の仕組みについて説明しました。ハミング符号の符号ビットとシンドロームテーブルのビット数を増やしたものが、BCH符号になることがおわかりいただけたかと思います。ただし今回の記事では、シンドロームテーブルは既に用意されている値を使い、このテーブルの求め方や、必要な符号ビットのビット数の求め方などについては解説していません。それは、メモリなどにエラー訂正の仕組みが内蔵さている場合には、このテーブルなどは予め用意されているので求める必要がないからです。もし一からプログラムなどでこのエラー訂正のコードをユーザー自身で書く場合には、符号理論に関する参考書などを参考してください。