熱設計について（熱の移動編）

はじめに

前回は、熱設計の基本フローの内容でしたが、今回はもう少し熱設計の知識としてデバイスが実装された基板上での熱について少し詳細を取り扱ってみようと思います。

 

熱の移動について

まず初めに触れていくのはデバイスで発生した熱がどのように移動（経路）していくかについてです。基板上での熱の移動は以下の3つの経路があります。

• 伝導による移動

• 対流による移動

• 放射による移動

それぞれの移動経路については以降で解説していきたいと思います。

 

伝導による移動

 

 

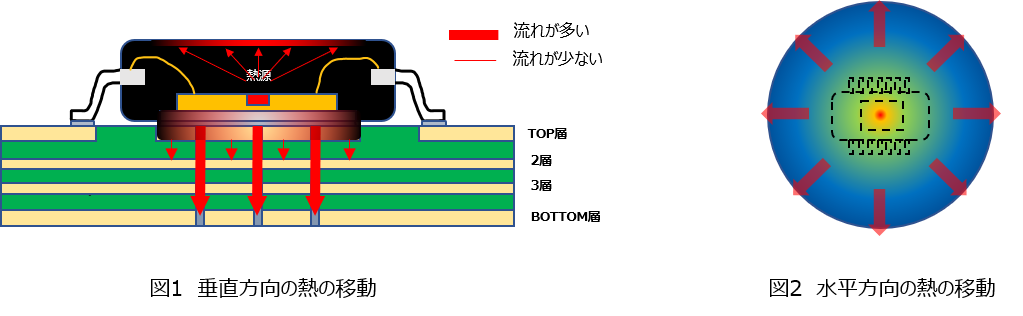
熱は熱伝導性の物質に沿って移動します。基板内では熱伝導率が最も大きい部分（銅箔、サーマルビア）に移動します（図1）。また、水平方向へは同心円状に熱が拡散します（図２）。熱の移動しやすさは熱経路の面積にも影響を受け、狭い経路よりも広い経路のほうに移動します（図3）。ホースで水を送るケースを想像するとイメージしやすいのではないかと思います。太いホースでは送り出す側の水の圧力がかかりにくく、細くなればなるほど圧力が増加します。熱の移動も水と同じように考えることができます。

 

 

対流による移動

 

 

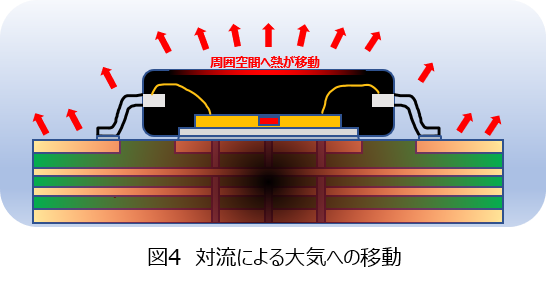
熱は物質の表面から静止状態または流動状態の空間（空気）へ移動します（図4）。流動している空気に対しての熱の移動は、計算での予測が非常に複雑で扱いが難しいため、今後本稿では静止状態の空気についてのみ扱うこととします。空気の流動がある（自然対流や強制対流）場合については、熱の移動が大きくなることで冷却が早く進み、熱源の温度が下がる方向になります（最終的にマージンと考える）。

 

放射による移動

 

 

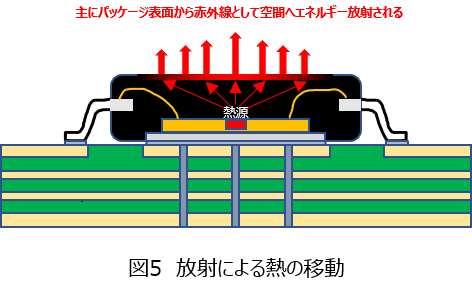
熱は物質表面から放射エネルギー（主に赤外線）として周囲空間へ移動します（図5）。放射による熱の移動量は複雑で扱いが難しいため、本稿ではマージンとして考え、直接扱うことをしません。最終的に熱の総移動量への影響としては熱量、放射する面積に依存するため、小さな基板、小さなパッケージのデバイスであれば誤差要因としては小さくなります。

 

熱抵抗について

次に熱の移動しやすさを示す熱抵抗について触れていきたいと思います。以下図6の電気回路のように熱抵抗は抵抗、熱源からの熱量（損失）を電流源として表現することができます。

 

 

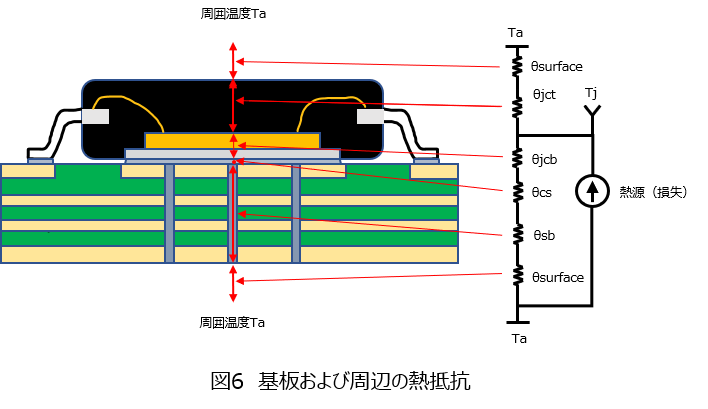
図6での各パラメータを以下で説明していきます。

・ジャンクション-パッケージ表面間の熱抵抗　θjct

多くの場合、データシートに記載されています。（JEDEC標準にて規定された環境下での測定値）

・ジャンクション-放熱パッド間の熱抵抗　θjcb

上記θjctと同様にデータシートに記載されていることが多いです。

・放熱パッド-基板放熱面間の熱抵抗　θcs

放熱用パッドを持つデバイスにおいてパッド面積の50%以上がハンダで接続されている場合はほとんど無視できる値です。

・基板の熱抵抗値　θsb

放熱がヒートシンクの場合、市販品であれば製品のデータシートにθsaとして規定値が存在します。θsaはヒートシンクの放熱フィンから大気へ放熱する際の熱抵抗となりますので扱い異なっています。θsbはPCB内部への熱伝導に対する熱抵抗で、基板表面からは大気へ放熱されるため、別途この熱抵抗値を求めます。また、θsbは基板内部の構成（層数、銅箔厚、サーマルビア数等）によって変化する値ですので、以降で説明する方法により計算する必要があります。

・基板表面から周囲の空気への熱抵抗　θsurface

周囲の空気は静止状態を想定します。

 

熱伝導率について

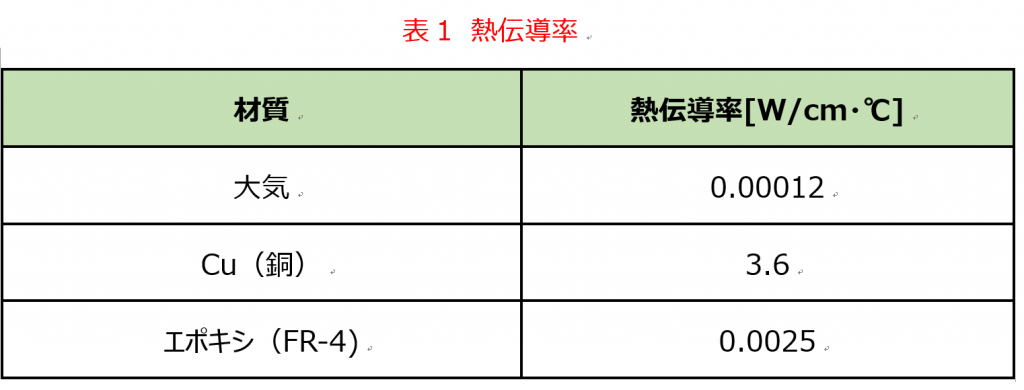
熱伝導率については一般的な値としておおよそではありますが以下の値を目安としています。これらの値は本稿の以降の計算でも使用しています。

 

熱抵抗の計算

物質内の伝導による熱抵抗について

物質内での熱の伝導における温度変化ΔTは（1）式より求められます。

 

 

 

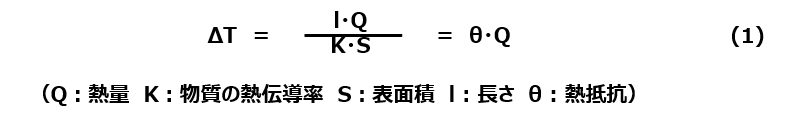
上記（1）式から熱伝導率が大きいほど熱抵抗値が小さくなることがわかり、より熱を伝えやすくなります。また、物質面の面積が大きいほど同じように熱抵抗値は小さくなります。ここから、熱伝導率の大きい物質でより広い面積を構成することで、効率よく熱を伝えることができることがわかります。（1）式と下図から垂直方向の熱抵抗については以下のようになります。

 

 

L=W=2.54mmの条件で、35um厚の銅層と1.5mm厚のエポキシ樹脂（FR-4）層の熱抵抗θはそれぞれ以下となります。

35um厚の銅：θ = 0.035/(0.36×2.54²) = 0.00015[℃/W]

エポキシ樹脂（FR-4）層：θ = 1.5/(0.00025 x2.54²) = 9.3[℃/W]

また、同様に水平方向の熱抵抗については以下のようになります。

 

 

同様にL=W=2.54mmの条件で、35um厚の銅層と1.5mm厚のエポキシ樹脂（FR-4）層の熱抵抗θはそれぞれ以下となります。

35um厚の銅：θ = 1/(0.36×0.035) = 79.4[℃/W]

エポキシ樹脂（FR-4）層：θ = 1/(0.00025 x1.5) = 2667[℃/W]

同じ条件で比較すると垂直方向の方が熱は移動しやすいことがわかります。

また、基板には熱の移動をスムーズにするためにサーマルビアを設置することがあります。このサーマルビアの熱抵抗は以下のように求めることができます。

 

ただし、実際にはサーマルビアは内部が均一面でない場合が多いため、計算値よりも大きくなる場合があります。

 

対流による物質表面から大気中への熱抵抗

次に対流による熱抵抗を計算します。熱の移動での温度変化ΔTは以下の（５）式で表されます。

 

 

 

上記（５）式は物質の表面からの放熱であるため材質には関係がない関数となります。(5)式から以下のように基板―周囲空間間の熱抵抗値が求まります。

 

 

物質間の熱の移動

ここで異なる材質の物質の面同士が接しているところでの熱の移動について触れていきたいと思います。熱の移動は以下の2つのルールがあります。

①　物質面には同じ量の熱流が生じます。

②　①で均一な材質で構成される層での温度上昇は各々の材質と厚さに依存します。

そのため、基板内の熱抵抗値は各層で計算される必要があります。

 

基板内の熱抵抗のモデル化について

先で触れた基板内の熱抵抗θsbについては以下の図10のように単位区画（0.1inch=2.54mm）の熱モデルで考えていきます。まずは基板内の熱の移動をイメージし、単位区画での熱抵抗値を計算していきます。単位区画での熱モデルは以下の手順でモデル化をしていきます。

①　デバイスの放熱パッド面積と同じ面積の円を設定する（図11）

②　①で設定した円に対して同心円状に等間隔（0.1inch=2.54mm）の帯を作成する（図12）

③　②の帯を展開して直方体モデルを作成する（図13）

④　各層毎に②、③と同じ手順でモデルを作成する

 

 

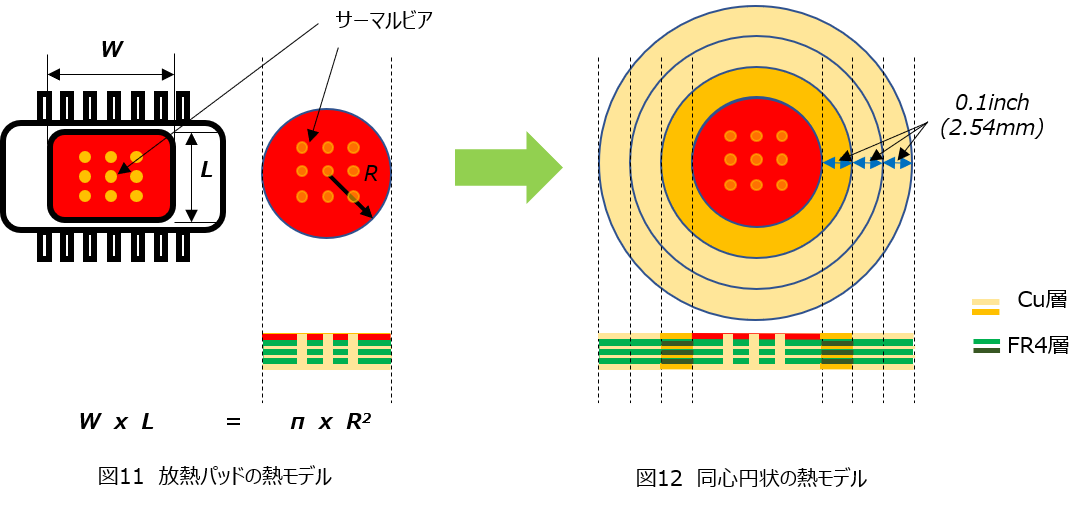
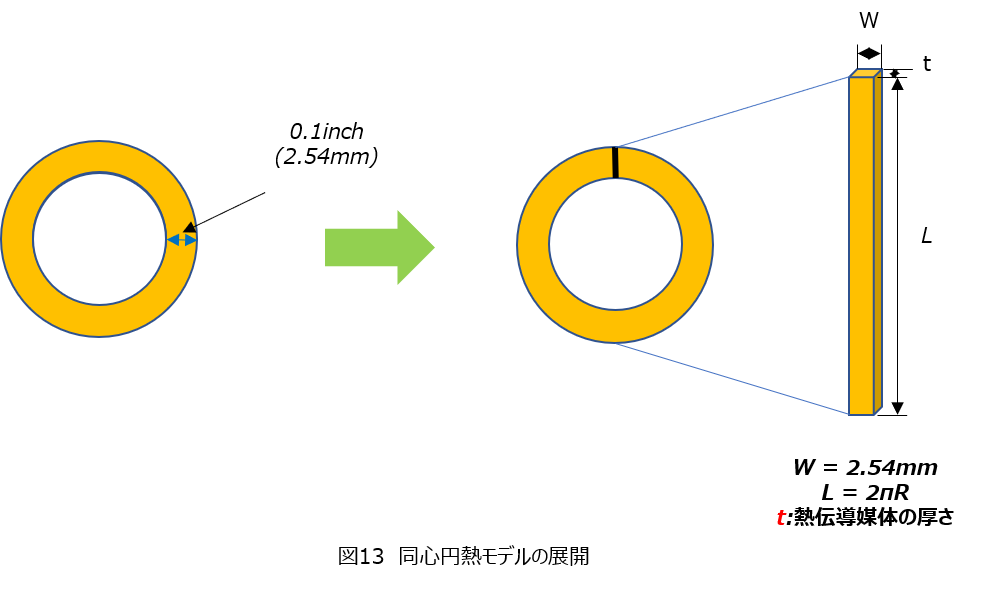
作成したモデルから水平、垂直方向および対流による熱抵抗を式(2)、(3)、(4)、(6)から計算していきます。ここでのポイントは水平方向には同心円上にモデルが形成されるため、外側に行くにしたがって外周が大きくなり、その結果、面積が大きくなることで熱抵抗が小さくなっていきます。作成した熱モデルのイメージは図14の右のようになります。

 

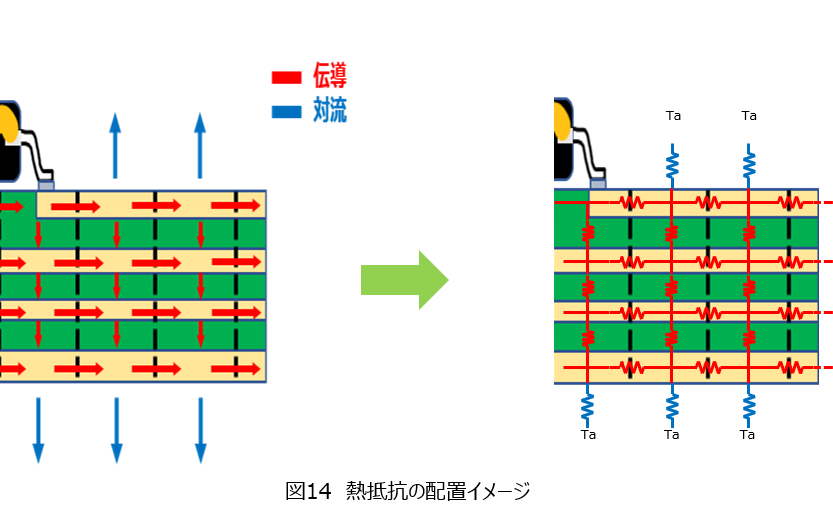
まとめ

これまでのまとめは以下となります。

・熱の移動経路として、3つあるが伝導と対流（静止した大気）のみ扱う（放射で移動する熱はマージン）

・熱は熱伝導率が大きく、広い面ほど伝わりやすい

・熱の移動は水平方向よりも垂直方向を経由したほうが効率よく熱を移動させることができる

・電子基板内での多くの場合、熱は熱伝導率が最も大きいCu層を経由して移動（拡散）する

・基板内の熱抵抗値は熱モデルとして同心円のイメージで単位区画当たりの面積から算出

・熱源から遠ざかるほど熱抵抗は小さくなっていく

 

次回の予定

今回は熱設計を行う上で重要な内容として熱の移動と熱抵抗について触れていきました。次回からは、最終的な目標として電気回路シミュレータによる熱回路網解析での評価についての実例をご紹介する予定です。実際の基板でのレイアウト、実装状態に則した条件にてシミュレーションを実施した結果と実測値の比較をしてみてどの程度の精度があるのかを検証していきたいと思います。

製品をお探しの方や不明点をお持ちの方は以下よりお問い合わせください。

ルネサス
メーカーページはこちら