- 公開日:2025年08月13日
- | 更新日:2025年10月28日
いまさら聞けない!暗号技術の基礎 Part1
情報セキュリティとは
情報セキュリティとは、各製品が扱うデータや情報を他者から守ることを言います。情報セキュリティというと、実際には、紙での資料なども入ってくるのですが、本記事ではデータに特化したサイバーセキュリティの観点で説明します。
具体的にはどうやって守っていくのか、ということを説明します。そこで重要なのが、情報セキュリティの三要素に、機密性、完全性、可用性というものがあります。

まず、機密性は、許可されていない人がデータにアクセスできないことです。万が一盗聴されても、データが漏れないようにするために、通信内容を暗号化し、製品内にデータを保存するときも暗号化し、アクセス制御のためにパスワードによる認証なども行い、データにアクセスすることを許可されていない人からデータを守ります。
次に、完全性は、データが改ざんや壊れずに完全なデータとして残っていることです。データが改ざんや壊れていなかを検証するには、メッセージ認証符号や署名といった技術を使用し検証することで、データの書き換えを許可されていない人からデータを守ります。
最後に、可用性については、許可された人が望んだ時にデータにアクセスできることです。データを失わないためにメモリを冗長化し、秘密分散といった技術が使われます。
表にまとめると下記の通りになります。

上記は、各要素に対して求められるものとそれを実現するための暗号技術を記載しています。
機密性に対して求められるものは、データの秘匿性であり、それを実現する暗号技術は、暗号化や認証となります。
完全性に対して求められるものは、データの正しさであり、それを実現する暗号技術は、メッセージ認証符号や署名となります。
可用性に対して求められるものは、データへのアクセスのしやすさであり、それを実現する暗号技術は、秘密分散となります。
※最後の可用性や秘密分散については、本記事では説明しません。
共通鍵暗号と公開鍵暗号
「機密性」に対して求められる「データの秘匿性」を実現する暗号技術である「共通鍵暗号と公開鍵暗号」および、関連する暗号技術について記載します。
【共通鍵暗号】
まずは、共通鍵暗号ですが、暗号化するときに使う鍵(秘密鍵)と復号するときに使う鍵が同じ暗号方式を「共通鍵暗号」といいます。秘密鍵暗号、対称鍵暗号と言ったりもします。
※本記事では各暗号方式で使用する他者に知られてはならない鍵を「共通鍵」という表現ではなく「秘密鍵」で統一しています。
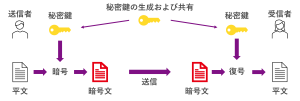
共通鍵暗号の仕組みとしては、
1.事前に送信者と受信者の間で、秘密鍵を共有して、使用する暗号アルゴリズムを決めておく。
2.次に送信者は平文と秘密鍵から暗号アルゴリズムを使って暗号文を生成し、暗号文を受信者に送る。
3.その後、受信者は共有しておいた秘密鍵と受け取った暗号文から暗号アルゴリズムを使って復号し、平文を生成する。
といった流れになります。
その共通鍵暗号ですが、大きくストリーム暗号とブロック暗号に分類されます。
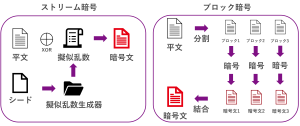
ストリーム暗号は、シードを擬似乱数生成器に入力して擬似乱数を生成し、平文をビットまたはバイト単位で擬似乱数との排他的論理和をとって暗号文を生成します。ですので、ストリーム暗号の性能は、疑似乱数生成器のアルゴリズムで決まってきます。シードと擬似乱数という言葉が出てきましたが、こちらについては後ほど説明します。
一方、ブロック暗号は、平文をある決まったサイズに分割して、その分割したブロック単位で暗号化し暗号文を生成します。ブロック暗号の暗号化については、いくつかのやり方があり、暗号化モードと呼ばれます。
暗号化モードには、ECBモードや、CBCモード、CTRモードなどのモードがあります。ですので、ブロック暗号の性能は、上図の「暗号」と書いてある部分の暗号化モードと暗号アルゴリズムで決まってきます。
共通鍵暗号をまとめると以下になります。

【乱数】
ストリーム暗号の性能は、擬似乱数生成器のアルゴリズムで決まると説明しましたが、乱数について少し深堀します。
次にどんな値になるか予測できない数字を乱数、乱数で構成された数字の列を乱数列と呼びます。

理想の乱数は、真の乱数となりますが、予測不可能性、再現不可能性がある乱数が真の乱数とされています。
具体的には、0と1の出る確率に偏りがあると、乱数の出方に偏りが出てきてしまうため予測しやすくなってしまいます。例えば、極端な話、4ビットの乱数があったとして、そのうちの3ビットが0に偏ってしまう場合、本来取りうる値が0~15に対して、1か2か4か8の値しか出なくなってしまい、予測しやすくなってしまいます。また、0と1が交互に出てしまうと簡単に予測できますし、交互になっていなくても、ある一定の繰り返しのパターンになっていると予測できてしまいます。真の乱数の生成方法については、回路内のノイズなどの再現できないものをベースに生成します。
また、乱数の乱雑さを示す指標をエントロピーといい、エントロピーが高いほど、理想的な乱数と言えます。ただ、現実的には、乱数のビット数が大きければ大きいほど処理時間がかかってしまいますので、現実的にはある一定のビット数で使用されます。NIST(アメリカ国立標準技術研究所)が推奨している暗号化用途におけるエントロピーは少なくとも128ビット以上が推奨されています。
【擬似乱数】
さて、真の乱数とエントロピーについて説明しましたが、ここからはストリーム暗号のポイントである擬似乱数について説明します。
擬似乱数は、シードと呼ばれる初期値を入力として、あるアルゴリズムによって生成された、一見、真の乱数に見える乱数となります。また、擬似乱数生成器は同じシードに対しては同じ擬似乱数を生成する性質を持っていて、シードがわからなければ予測不可能な性質を持つので、一見、真の乱数のように見えます。
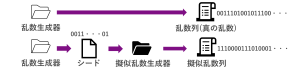
なぜ、真の乱数ではなく、擬似乱数を作っているのかというと、真の乱数は、回路内のノイズなどの再現できないものをベースに生成していきますので、エントロピーをある程度のビット数まで増やすのに時間がかかります。
一般的には、擬似乱数生成器による乱数生成の方が処理時間は速く、また、シードがわからなければ真の乱数と同じように扱えます。ですので、乱数生成器で真の乱数をあるビット数まで生成し、それをシードとして、擬似乱数生成器を使用して乱数を生成するのが、一般的であり効率的とされています。例えば、128bitの真の乱数を生成して、4倍の512bitの擬似乱数を生成するようなことをやったりします。
【ナンス】
さて、擬似乱数について説明しましたが、擬似乱数生成器はシードが同じなら同じ乱数列を出力する性質があるため、そのままでは同じシードを一度しか使えません。一つのシードから、複数の異なる擬似乱数を生成するために、一緒に擬似ランダム関数に入力する値をナンスと呼びます。また、ナンスは秘密にする必要はないですが、擬似ランダム関数も同じナンス、同じシードに対しては同じ擬似乱数を生成しますので同じシードに対して同じナンスを2回つかってはいけません。
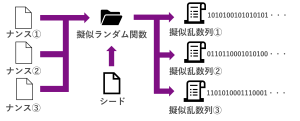
ここで、擬似ランダム関数という言葉が出てきましたが、ここでは、シードから擬似乱数を生成するものを擬似乱数生成器と呼び、シードとナンスなどの複数入力から擬似乱数を生成するものを擬似ランダム関数と呼んでいます。
ストリーム暗号の代表例として、ChaCha20を挙げましたが、ChaCah20では、擬似ランダム関数に、秘密鍵とナンスとカウンタを入力することで擬似乱数を生成し、その擬似乱数を平文と排他的論理和を取ることで暗号文を作り出しています。
【暗号化モード】
今までは、ストリーム暗号に関連する説明をしましたが、続いてブロック暗号に関連する説明をします。
ブロック暗号の性能は、暗号化モードと暗号化アルゴリズムで決まると説明をしましたが、暗号化モードについて少し深堀します。暗号化モードは方式によって安全性や性能が異なります。ここでは、ECB(Electronic Code Book)モード、CBC(Cipher Block Chaining)モード、CTR(Counter)モードを紹介します。
まずECBモードですが、平文をブロックに分割して、それぞれを暗号化して暗号文を作る方式です。
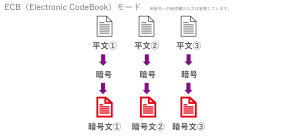
ただ、ECBモードは、入力の平文が同じであれば、出力の暗号文も同じものが生成されてしまうため、データのパターンは隠すことができず、現在では安全なアルゴリズムではないとされ使われていません。具体的にどういうことかを以下で説明します。
こちらのペンギンの画像は、マクニカの公式キャラクターの「タネペン」といいます。

このタネペンとタネペン文字のビットマップのヘッダデータを取り除いて、画像データ部分のみを、ECBモードで暗号化した場合と、CBCモードで暗号化した場合の画像になります。見た通り、ECBモードではうっすらタネペンが見えており、タネペン文字に至っては、文字を隠しきれていないことがわかります。一方、CBCモードはしっかりと隠しきれています。
ウェブ会議等で使用されているZoomも、2020年4月よりも前のバージョンでは暗号化モードにECBモードが使われていていましたが、現在ではしっかりと改修されています。2020年3月、4月辺りといえば、ちょうどコロナ化で、ウェブ会議等でZoomを使用していた方もいるかと思いますが、その当時使用していた方は、画面共有していた内容を、横からうっすらとみられていたかもしれません。
次にCBCモードですが、ECBとは違い、平文ブロックをそのまま暗号化するのではなく、ひとつ前の暗号文のブロックと排他的論理和を取ってから暗号化します。
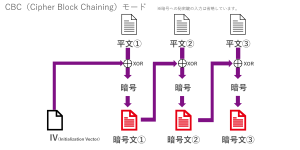
先頭の平文ブロックにはひとつ前の暗号文がないので、初期化ベクトルIVを使用します。IVは暗号の際に与えるブロックと同じビットサイズの値になります。IVは暗号文と一緒に復号相手に一緒に渡すため公開される情報となりますが、予測できないランダムな値を、擬似ランダム関数などを使用して生成します。仮に平文①と平文②が同じ内容だったとしても、暗号文①と平文②を排他的論理和してから暗号化するため、ECBモードと違い、暗号文①と暗号文②は異なる値になります。
最後にCTRモードですが、ブロック暗号を使って擬似乱数を生成し、ストリーム暗号のように利用するモードになります。
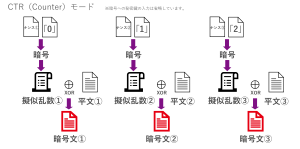
例えば、ブロックを半分に分けて片方をナンス、もう片方を0から始まるカウンタとします。ナンスは説明した通り、秘密にする必要はありませんが同じ値を使わないようにします。カウンタは1ブロックごとに値を一つずつ増やします。各ブロックを秘密鍵で暗号化し、出力された暗号文を擬似乱数とみなして、平文と排他的論理和を取って暗号文を作ります。ナンスは暗号文と一緒に通信相手に渡します。
CBCモードは、先頭から順番に暗号文を作らないと処理できませんが、CTRモードは、平文をブロックに切り出した後は、暗号文を作るのに並列に処理することができます。
ブロック暗号の代表例として、AESを挙げましたが、各暗号化モードの「暗号」部分がAESなどのアルゴリズムになります。
【公開鍵暗号】
今までは、共通鍵暗号とそれに付随する技術について説明しましたが、続いて、公開鍵暗号について説明します。
共通鍵暗号と同じような形で書くと下記の通りとなります。
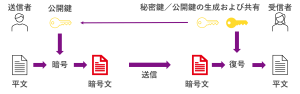
事前に暗号アルゴリズムを決めておき、受信者側で秘密鍵と公開鍵を生成して、送信者に公開鍵を渡します。
次に、送信者は平文と公開鍵から、暗号アルゴリズムを使って暗号文を生成し、暗号文を受信者に送ります。
その後、受信者は生成した秘密鍵と受け取った暗号文から暗号アルゴリズムを使って復号し、平文を生成します。
公開鍵暗号では暗号化するときと、復号するときに異なる鍵を使うのがポイントです。暗号化用の鍵は誰にも知られてもよい公開鍵、復号用の鍵は自分しか知らない秘密鍵になります。秘密鍵と公開鍵は密接な関係があり、大体の公開鍵暗号は秘密鍵から公開鍵を生成します。逆に公開鍵から秘密鍵を生成することはできないため、公開鍵を他人に知られても問題はなく、秘密鍵をこそこそと渡すような苦労はありません。この鍵の取り扱いの違いが、共通鍵暗号との最大の違いになります。
公開鍵暗号の鍵が公開しても問題ないとされている理由は、一方向性関数によって成り立っているからです。一方向性関数とは、計算は容易ですが逆計算が非常に困難な関数のことです。
例えば、RSA暗号は巨大な素数の積を利用しており、積を求めるのは簡単だが、逆に素数を特定するのは非常に難しいということで安全性を確保しています。また、公開鍵は誰が見ても問題はないという性質から、不特定多数と鍵のやり取りを行う場合は、共通鍵暗号と比べ、公開鍵暗号の方が有利となります。公開鍵暗号の代表的なアルゴリズムとしては、RSA暗号やECCなどがあります。

【ハイブリッド暗号】
最後にハイブリッド暗号について説明します。
共通鍵暗号に対して、公開鍵暗号は暗号化で使う鍵を公開してよいのが利点ですが、一般的に公開鍵暗号は、共通鍵暗号に比べて処理速度がかなり遅いです。そこで、共通鍵暗号の処理速度と公開鍵暗号の鍵管理の利点を組み合わせたハイブリット暗号というものがあります。ハイブリット暗号の暗号アルゴリズムは、共通鍵暗号で使用する秘密鍵だけを公開鍵暗号のアルゴリズムで暗号化し、平文は共通鍵暗号のアルゴリズムで暗号化します。
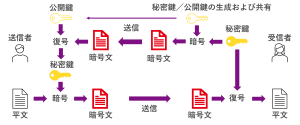
事前に暗号アルゴリズムを決めておき、受信者側で秘密鍵と公開鍵を生成して、送信者に公開鍵を渡します。
次に、受信者は公開鍵で秘密鍵を、公開鍵暗号アルゴリズムを使って秘密鍵の暗号文を生成し、送信者に送ります。
次に、送信者は公開鍵と暗号文から、公開鍵暗号アルゴリズムを使って秘密鍵を生成します。
送信者は平文と復号した秘密鍵から、共通鍵暗号アルゴリズムを使って暗号文を生成し、暗号文を受信者に送ります。
その後、受信者は秘密鍵と受け取った暗号文から共通鍵暗号アルゴリズムを使って復号し、平文を生成します。
繰り返しになりますが、ハイブリット暗号は共通鍵暗号の処理速度と公開鍵暗号の鍵管理の利点を組み合わせた方式となります。ですので、鍵を公開して、不特定多数とやり取りしたいが処理速度も重視したい、といった時に使用されます。
【最後に】
「いまさら聞けない!暗号技術の基礎 Part1」はここまでとなります。「いまさら聞けない!暗号技術の基礎 Part2」では「メッセージ認証符号や署名」、関連する暗号技術について記載します。(2025年10月公開済み いまさら聞けない!暗号技術の基礎 Part2 | 組込み技術ラボ)
