【初心者向け】デジタル半導体の基礎　～2進数と16進数～

近年、デジタル半導体の市場は世界的に拡大傾向にあり、AIやIoTから自動車に至るまで

様々な分野の産業で、その重要性は増してきています。

本ブログでは、デジタル半導体を使用する上で欠かせない2進数と16進数について説明していきます。

2進数と16進数の概要

我々が普段使用している「数値」は0~9までの10種類の文字で表記をしており、これを10進数と呼びます。

10進数の場合、0,1,2, … ,9まで数えると次の数値は桁が上がり十の位が”1″、一の位は再び”0″に戻る、

すなわち”10″となるのはみなさんご存じの通りです。

 

【2進数の概要】

2進数では0,1の2種類の文字で表記を行います。

0,1まで数えると次の数値で桁が上がり、二桁目は”1”、一桁目は再び”0″に戻り”10″となります。

つまり、2進数の”10″は10進数の”2″を表しています。

次の数値は”11″（10進数：3）、その次は桁が上がり”100″（10進数：4）と表記します。

 

【16進数の概要】

16進数では、0~9までの文字にアルファベットのA,B,C,D,E,Fを加えた16種類の文字で表記を行います。

0,1,2, … ,9まで数えると次の数値からはアルファベットを使用し、A,B, … ,F(10進数：15)と表記します。

次の数値で桁が上がり、二桁目は”1”、一桁目は再び”0″に戻り”10″となります。

つまり、16進数の”10″は10進数の”16″を表しています。

2進数と16進数の存在意義

【2進数の存在意義】

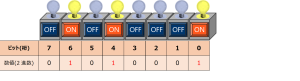
2進数は0と1の2種類の文字で構成されているため、電子回路でのスイッチの状態を直接表現するのに非常に適しています。

スイッチOFFを”0”、スイッチONを”1”とすると、トランジスタのスイッチング動作(電流のオン/オフ)を利用して

電子回路の状態を0,1で表現することができるようになります。これを２進数の各桁に見立てると、

以下のように数値で各スイッチ(トランジスタ)の状態を表現できるようになるのです。

 

初心者方々の中には、トランジスタとは何ぞや？と思われた方も多いと思いますので、トランジスタについて少し補足します。

 

<トランジスタについての補足>

トランジスタとは電子回路上で電気の流れを制御できる素子です。

上記の説明にも記載した通り、スイッチング(電流のオン/オフ)を行うことができます。

以下の回路記号で表す、Nチャネル接合型FET と呼ばれるトランジスタを例に説明します。

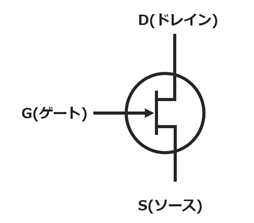
Nチャネル接合型FETには以下の特性があります。

・G端子に規定の電圧をかけることで、D端子からS端子に電流が流れる。

・G端子に電圧をかけない、または規定の電圧に満たない場合、D端子からS端子に電流は流れない。

つまり、G端子に電圧をかける/かけないを切り替えることで、D端子・S端子間に電流を流す/流さないのスイッチングが可能なのです。

 

D端子・S端子間に電流を流す/流さない、のON/OFF状態を0,1で表現することができる、というのが２進数の利点というわけです。

 

【16進数の存在意義】

16進数は2進数を圧縮して効率的な表現をするのに非常に役立ちます。

というのも、1桁の16進数は4桁の2進数に等しいため、以下表の通り16進数の方が少ない文字数で表現できるからです。

(10進数と比較しても、より少ない文字数でより大きな数値を表現できますね。)

10進数	2進数	16進数
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F

 

進数の変換方法

2進数⇔16進数の変換、2進数⇔10進数の変換方法についてそれぞれ説明します。

以下、頭に「B’」が付いた数値は2進数、「H’」が付いた数値は16進数を表します。

例)

B‘11：2進数の”11”なので10進数の”3”です。

H’11：16進数の”11”なので10進数の”17”です。

 

【2進数⇒16進数の変換】

2進数の低い桁から4文字ごとにそのまま1文字の16進数に変換することができます。

例えば、B’11110000を変換する場合、“1111“と”0000”に区切って考えます。

B’1111 = H’F

B’0000 = H’0

ですので、B’11110000 = H’F0と変換することができます。

注：桁が4の倍数でない場合は、低い桁から4文字ずつ区切る必要があります。

例えばB’110000の場合はB’11とB‘0000に区切って考え、H’30としましょう。

 

【16進数⇒2進数の変換】

2進数⇒16進数とは逆で、16進数1文字ごとに4文字の2進数に変換することができます。

例えば、H’C3を変換する場合、

H’C = B’1100

H’3 = B’0011

ですので、H’C3 = B’11000011と変換することができます。

 

【2進数⇒10進数の変換】

2進数各桁の2のべき乗(2^桁数 )に各桁の数値( 0もしくは1)を掛け、それぞれ積を求めます。

その積をすべて足していくことで10進数へ変換することができます。

分かりにくいと思いますので、以下に例を示します。

 

例えば、B’10101010の場合、各桁の数値、2のべき乗(2^桁数 )はそれぞれ以下となります。

桁	7	6	5	4	3	2	1	0
2進数	1	0	1	0	1	0	1	0
2^桁数	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0

 

したがって、

B’10101010 =(2^7×1)+(2^6×0 )+(2^5×1 )+( 2^4×0)+(2^3×1 )+(2^2×0)+(2^1×1 )+(2^0×0)

=128+0+32+0+8+0+2+0

=170

となります。これで10進数に変換することができました。

【10進数⇒2進数の変換】

対象の10進数に対して、商が0になるまで2の割り算を繰り返します。

そのときの”あまり”を低い桁から並べていくと2進数に変換することができます。

 

さきほどの”170”が、B’10101010に戻るか確認してみましょう。

170÷2 = 85あまり0　⇒0桁目

85÷2 = 42あまり1　⇒1桁目

42÷2 = 21あまり0　⇒2桁目

21÷2 = 10あまり1　⇒3桁目

10÷2 = 5あまり0　⇒4桁目

5÷2 = 2 あまり1　⇒5桁目

2÷2 = 1 あまり0　⇒6桁目

1÷2 = 0あまり1　⇒7桁目

順番に並べるとB’10101010となっていますので、もとの2進数に戻っていますね。

 

【おまけ】

10進数⇒16進数の変換は2進数を経由することで変換することができます。

16進数⇒10進数の変換は2進数を経由してもよいのですが、

2のべき乗の足し算を応用して16のべき乗をすべて足す方法が便利です。

H’A0Fの場合、

H’A0F　= (16^2×10) + (16^1×0) + (16^0×15)

=2560+0+15

=2575

となります。

 

まとめ

本ブログでは、デジタル半導体の利用に不可欠な2進数と16進数について詳しく解説しました。

デジタル技術が進化する現代において、これらの基本的な数値表現の理解は、

エンジニアリングやプログラミングの基礎を形成する上で非常に重要です。

学生の方、エンジニアになりたての方、リスキリング中のエンジニアの方、

みなさまの専門性を高める第一歩となれば幸いです。