チラシ・郵便物判定システムを作ってみた ～アルゴリズム編～

これまでは、ソフトとハードの作成について記載してきましたが、実は最も重要な部分である判定アルゴリズムに関する記載をしてきませんでした。この章では、最も時間をかけたといっても過言ではない、判定アルゴリズムの作成について記載していきます。

カラーセンサの校正

まずは、前回までに作製した筐体を用いてカラーセンサの単体テストを行いました。すると、、

 

カラーセンサごとにRGB値に大きく乖離がある、、、

 

という不具合が発生し、中には2倍以上の差があるものもありました。

原因は、はんだ付けや筐体の傾きなどハード面の誤差の蓄積によるものだと考えられます。ハード面では考えうる原因の要素が多く、修正が困難であると考えたため、ソフト面でカラーセンサの校正を行うことにしました。

 

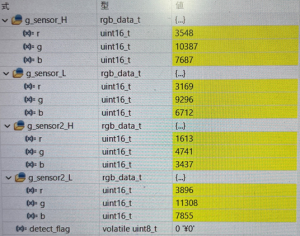
具体的には、4つのカラーセンサで赤・緑・青のコピー用紙をそれぞれ5回測定し、各カラーセンサにおける赤・緑・青の平均値を算出しました。以下の画像はセンサID1での取得結果になります。これを、4つのカラーセンサ全てでRGB値の取得を行いました。その後、1つのカラーセンサを基準として選択し、基準のカラーセンサに合わせる形式で他のカラーセンサのRGB値を倍率補正することで校正を行いました。

 

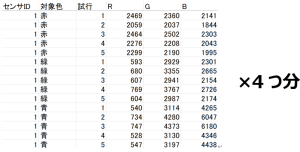
最終的な測定結果は以下になります。特に、センサID2・ID3とセンサID4に大きな乖離があることがわかります。今回はセンサID4を基準に設定し、下記表のゲインに従って各センサの倍率補正を行いました。

 

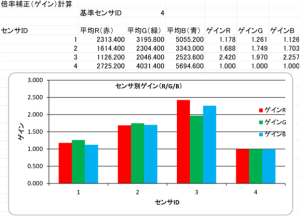
判定方針の決定

ここから判定アルゴリズムの作成について詳細に説明していきます。

まずは、郵便物とチラシの特徴を把握し、判定における着目点を決定しました。私が考えた特徴は以下になります。

 

 

上記の特徴から着目点を以下の2つに決定しました。

 

1. 紙面の全体的な色の均一性と多様性
2. 紙面の上下・左右方向の色の均一性と多様性

 

紙面の全体的な均一性と多様性に加え、上下・左右方向の観点を追加することで、より郵便物とチラシの差を明確に捉えることができると考えました。

参考にした指標

RGB値では色の特徴量を直感的に把握しにくいと考えたため、私はHSV色空間を参考指標として使用することにしました。

HSV色空間とは、RGBから算出される指標であり、色を人間の感覚に近い要素で表現するために色のニュアンスを定量化したものです。以下の3つで構成されます。

 

1. Hue（色相）：色の種類（赤、緑、青など）を示し、0~360°で表現する
2. Saturation（彩度）：色の鮮やかさを示し、0~1で表現する
3. Value（明度）：色の明るさを示し、0~1で表現する

 

今回は、Hue（色相）において判定に有効なデータを得ることができなかったため、彩度・明度の計算式のみについて説明していきます。

 

 

測定開始

お待たせしました。ここからは実際の測定結果を示していきます。

サンプルはこの日のために約2か月貯めてきたチラシ51枚、郵便物9枚を使用して測定を行いました。郵便物は意外と少なかったです。

判定ボックスに1枚ずつ投函し、取得したRGB値をもとに計算したデータは以下になります。

 

もはや見えないですね。笑

これらのデータからグラフを作成しました。グラフは軸の組み合わせを何度も変更し、様々なパターンのグラフの比較を行い、有効なしきい値を模索しました。

 

実際にしきい値判定に使用したグラフを示していきます。

以下は、横軸が紙面全体の色鮮やかさの分散、縦軸は紙面全体の色の明るさの分散を示しています。郵便物は彩度の分散が0.007以下の範囲に収まっています。こちらのグラフから彩度の分散においては、郵便物の方が小さいことがわかります。

 

以下は、横軸が紙面左側の色鮮やかさ、縦軸は紙面右側の色鮮やかさを示しています。このグラフは軸が左右の平均を示しているので、左右で色鮮やかさに差が無いほど、y=xのグラフの近辺にデータが集中するようになっています。左の郵便物のグラフはy=xに集中しており、これは仮説通りであるといえます。このブラフから、傾きをしきい値の設定範囲として使用しました。

 

 

以下は、横軸が紙面左右の色の明るさの差分、縦軸が紙面左右の色鮮やかさの差分を示しています。左の郵便物のグラフは、左右彩度差分が0.05以下にデータが集中しています。こちらのグラフも郵便物の方が分散が小さい結果となりました。

 

 

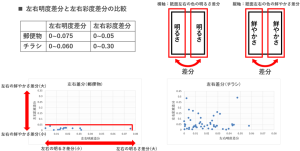
以下は、横軸が紙面上下の色鮮やかさの差分、縦軸が紙面左右の色鮮やかさの差分を示しています。グラフより郵便物は、左右彩度差分0.05以下、上下彩度差分0.15以下に点在していることがわかります。こちらのグラフも郵便物の方が分散が小さい結果となりました。

 

 

そして、上記グラフの結果を組み合わせ、しきい値は以下に設定しました。

 

(0<左右明度差分<0.08 && 左右彩度差分<0.05) && (0<上下彩度差分<0.15)

&& (彩度の分散<0.009) && (0.94<(左側平均彩度÷右側平均彩度)<1.026)

 

これでやっと、判定アルゴリズムが完成しました！

気になるアルゴリズムの正確性についてですが、それは次の最終話で発表させていただきます！

判定アルゴリズムまとめ

本来ならAIにデータを読み込ませてしきい値を決定することが一般的であると思いますが、今回はそれをすべて私自身で行い非常に大変でした。笑

ただし、これこそが製作実習の醍醐味であると思います。

次回「第５話：集大成」