ハミング符号の大枠を掴もう　誤り検出・訂正基礎講座 　　　第2回

はじめに

ウェブ検索などでハミング符号について調べてみると、検査行列、生成行列、ハミング距離など聞き慣れない単語や数学が出てきて、理解するのには結構な時間を要してしまうと思います。この記事は、そんな小難しい理論を排除し、ハミング符号の大枠をなんとなく理解することを目的としてまとめています。この記事の内容でECCメモリなどで使われているハミング符号が、どのような計算をして誤りを検出しているのか、イメージを掴んでいただけると思います。

前回の記事：パリティチェック・チェックサムとは？　誤り検出・訂正基礎講座 第1回

XOR演算とAND演算

ハミング符号の説明の前に論理演算のXOR演算について簡単に説明します。このXOR演算の特徴を知っているとハミング符号の理解が早くなります。

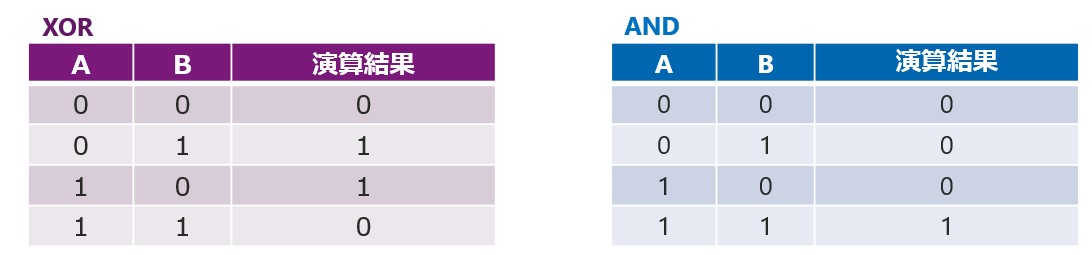
上がXORとANDの真理値表となります。XORの演算結果は「XOR=ビット反転」と覚えます。「Bが1のとき、Aの値を反転する」ということです。さて、このXORとANDはどこで使うことが多いでしょうか。ANDやORはよく使うけど、XORはあまり使ったことがないとう方も多いのではないでしょうか。しかし、XORには、ANDやORなどの論理演算には無い大きな特徴を持っています。それは、XORはデータを完全に復元可能ということです。例えば、以下のデータAとBのXORとANDの結果をそれぞれ算出します。

もし、このときBの値がわからなくなってしまったらどのように復元しますか？

XOR演算の場合、AとOUTでXORすればBがわかりますが、ANDの場合逆算すると一番右のビットが判別できなくなってしまいます。このような性質から、XORは暗号化、復号化によく用いられます。

ハミング符号

ハミング符号は、データを送信する際に、本来のデータに一定の手順で計算したチェック用のデータを付加して送信することにより、受信側で受け取ったデータに誤りがないかどうかを検証することができるものになります。誤りがあった場合、1bitの誤りであれば訂正が可能となります。ハミング符号はある程度高速で処理ができるので、速度の要求されるECCメモリなどでよく使われています。

情報ビットと符号ビット

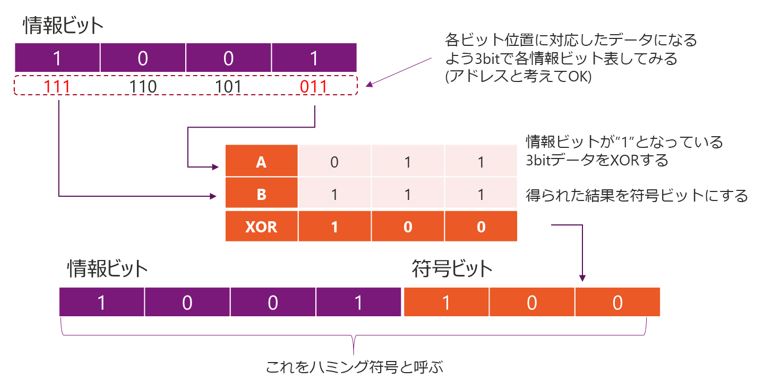
4bitのデータを例に、ハミング符号を説明したいと思います。以下のような4bitデータ”1001b”を送信するとします。(以下この4bitデータを情報ビットと呼びます。) ハミング符号は、一定の手順で計算したチェック用のデータを付加して送信する必要があります。まず、情報ビットを以下のように各ビットの位置に対応したデータになるよう3bitで表します。(アドレスのようなイメージになります。) この情報ビットを左から111b, 110b, 101b, 011bと表したとします。そして情報ビットが1となっている3bitデータをXORします。つまり、111bと011bをXORします。結果は100bとなるので、これをチェック用のデータとして付与して送信します。この情報ビットと符号ビットを併せてハミング符号と呼びます。

 

エラー検出のためのXOR演算

先程符号ビットを算出したハミング符号を送信し、受信側は受け取ったデータをXORします。正常にデータの送受信ができている場合には、XORの結果が0,0,0となります。このとき符号ビットは3bitなので、左から100b, 010b, 001bとアドレスを振っておきます。符号ビットは特定の桁に一つだけ1が入っているものを用いると、計算上、都合が良いのでこのようにしています。

 

1bitのビット化け発生時

先程のハミング符号を送信し、受信側で情報ビットの”110”の箇所がビット化けした場合を見てみます。正常にデータを受信できた場合にはXORの結果は0,0,0となりますが、今回この0,0,0にさらに1,1,0がXORされるため、XORの結果は110となります。つまり、ビット化けした場所をXORの結果が示すことになります。これにより、ハミング符号は1bitのエラー訂正が可能となります。

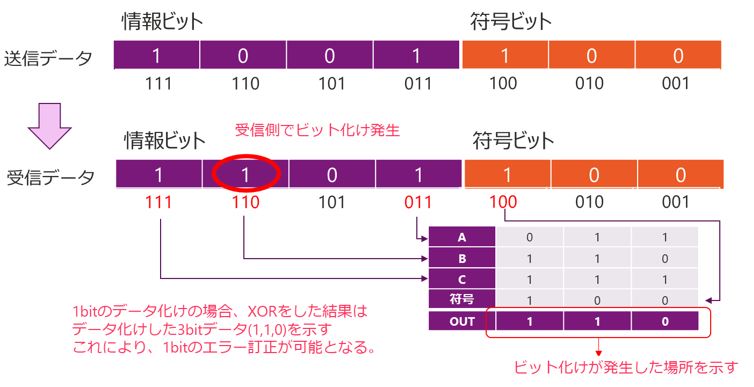
このビット化けは、符号ビットが化けたとしても同様の結果となります。

エンコードとデコード

ハミング符号では情報ビットをエンコードして、符号ビットを作成します。このエンコードには情報ビットに割り当てたアドレスビットを用いて行いますので、数式で表すと”情報ビット”と”アドレスビット”の行列の乗算になります。この乗算結果が符号ビットになります。

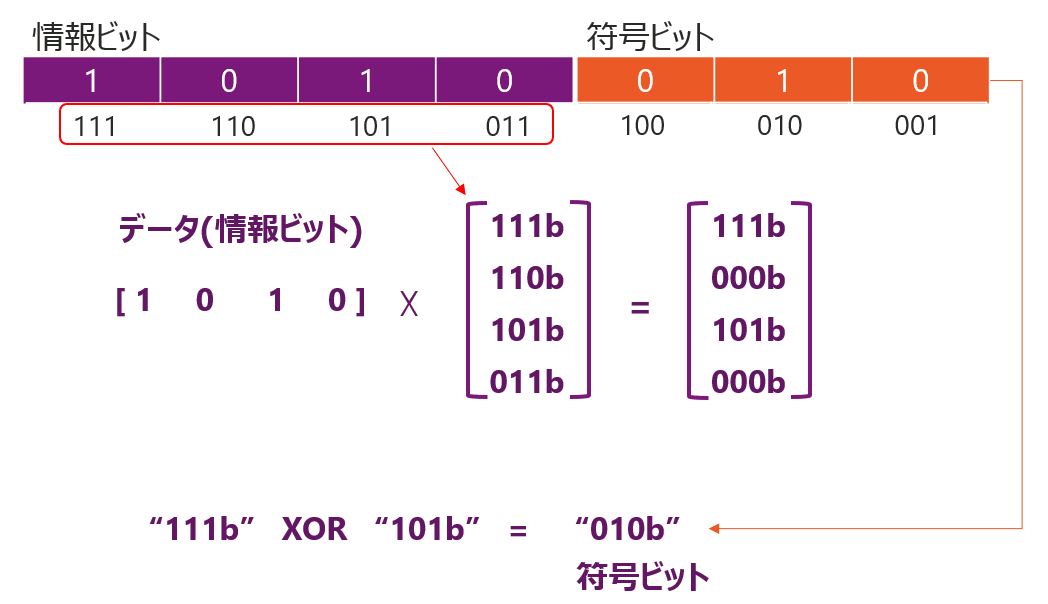
そして、エンコードされたデータをデコードして、格納されているデータの誤り検出/訂正を行います。デコードには情報ビットと符号ビットのアドレスビットを用います。数式で表すと、”情報ビット”と”符号ビット”に割り振られたアドレスビットを使った行列の乗算となります。アドレスビットのテーブルをシンドロームテーブルと呼びます。

ECCメモリなどのマニュアルを見ると、このテーブル(行列)が定義されていると思います。このテーブルがデータのエンコード、デコードを行うためのテーブルになっています。

さいごに

今回はハミング符号の仕組みについて説明しました。数式で理解しようとするとなかなか難しいハミング符号ですが、実際にはテーブルを用意して行列演算を行っているだけであることがわかると思います。そして、暗号化、復号化の世界でなぜXORが頻繁に使われているかの理由についてもなんとなくご理解いただけたかと思います。

しかし、ここで一つ疑問が残ります。ECCメモリなどでは「1bitのエラー訂正と、2bitのエラー検出が可能」と記載されていることが多いと思いますが、今回のハミング符号で2bitのエラーが起きた場合どうなるでしょうか。計算するとすぐわかるのですが、2bitのエラーが起きた場合には、デコード時に異なるエラー箇所が示されてしまい、エラー訂正が正しく行えません。この問題を解消するために拡張ハミング符号というものが用意されております。次回の記事ではこの拡張ハミング符号について解説したいと思います。

次の記事：拡張ハミング符号の仕組み　誤り検出・訂正基礎講座 第3回

ルネサス製品をお探しの方は、メーカーページもぜひご覧ください。

ルネサス
メーカーページはこちら